Giải mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thức trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập chuyên sâu.
Với đội ngũ giáo viên giàu kinh nghiệm, tusach.vn mang đến cho các em những lời giải chính xác, dễ hiểu, cùng với các phương pháp giải bài tập hiệu quả.
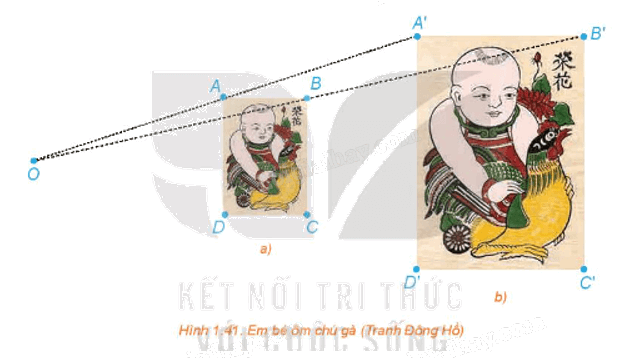
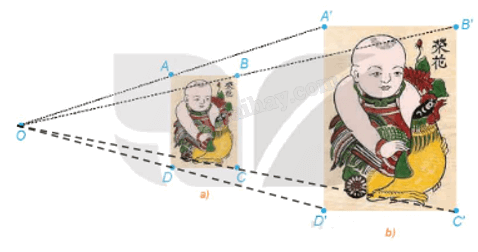
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
Câu hỏi
Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm nào? Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm nào?
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
- Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm O.
- Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm M.
Thật vậy, nếu M' là ảnh M qua phép vị tự \({V_{(O,{\rm{ }}k)}}\) thì \(\overrightarrow {OM'} = k\overrightarrow {OM} \Leftrightarrow \overrightarrow {OM} = \frac{1}{k}\overrightarrow {OM'} \). Điều này có nghĩa là M là ảnh của M' qua phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\).
Luyện tập 1
Chứng minh rằng, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất, phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
+ Phép vị tự \({V_{(O,{\rm{ }}1)}}\) biến điểm M thành điểm M' thỏa mãn \(\overrightarrow {OM'} = \overrightarrow {OM} \). Khi đó M' trùng với M. Do đó, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất.
+ Phép vị tự \({V_{\left( {o,-1} \right)}}\;\) biến điểm M thành điểm M" thỏa mãn . Khi đó O là trung điểm của MM". Do đó, M" là ảnh của M qua phép đối xứng tâm O hay phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Hoạt động 1
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Hãy tính các tỉ số \(\frac{{OA}}{{OA'}},\,\frac{{OB}}{{OB'}},\,\frac{{OC}}{{OC'}},\,\frac{{OD}}{{OD'}}\).
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Phương pháp giải:
Dựa vào định lí Thalès để chứng minh A, B, C, D lần lượt là trung điểm của A’O, B’O, C’O, D’O.
Lời giải chi tiết:
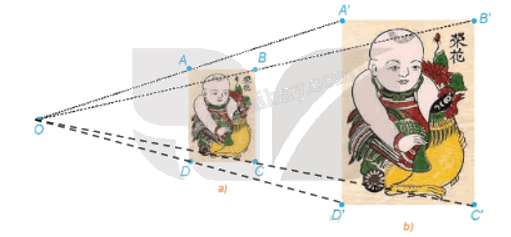
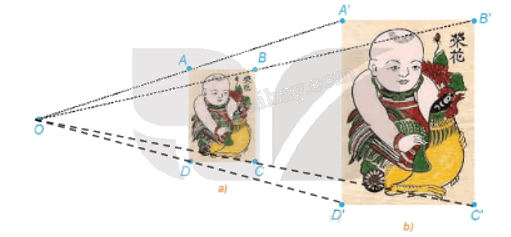
a) Gọi O là giao điểm của AA' và BB'.
Xét tam giác OA'B' có AB // A'B', theo định lý Thales, ta có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\)
Từ đó suy ra A, B lần lượt là trung điểm của OA' và OB'.
Gọi C" là giao điểm của BC và OC'. Vì BC // B'C' nên BC" // B'C'.
Xét tam giác OB'C' có BC" // B'C' và B là trung điểm của OB' nên BC" là đường trung bình của tam giác OB'C'. Suy ra và C" là trung điểm của OC'.
Mặt khác theo giả thiết ta có \(BC = \frac{1}{2}B'C'\). Do vậy C" trùng với C và C là trung điểm của OC'.
Chứng minh tương tự, ta được D là trung điểm của OD'.
Vậy các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Vì A, B, C, D lần lượt là trung điểm của OA', OB', OC', OD' nên
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\).
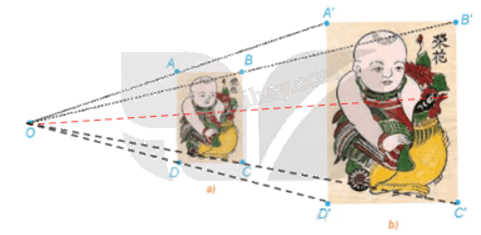
c) Dùng thước thẳng nối hai điểm tương ứng trên hai bức tranh, cụ thể, đầu mỏ trên của chú gà ở hai bức tranh, ta thấy đường thẳng này đi qua điểm O.
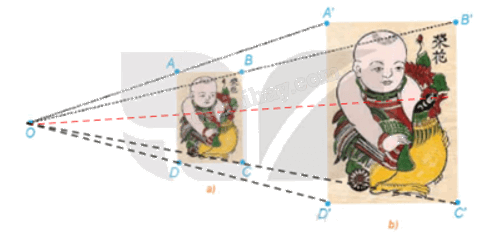
Vận dụng 1
Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.
Phương pháp giải:
Quan sát hình ảnh và tìm tỉ số k
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
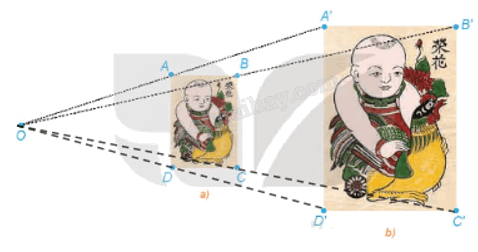
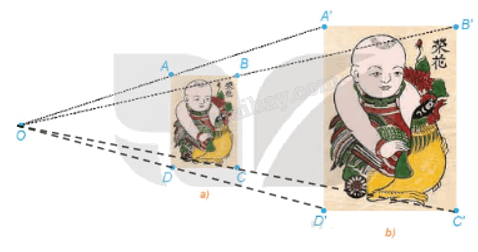
Ta có: \(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{OD}}{{OD'}} = \frac{1}{2}\) (theo HĐ1).
Suy ra \(\overrightarrow {OA'} = 2\overrightarrow {OA} ;\,\overrightarrow {OB'} = 2\overrightarrow {OB} ;\,\overrightarrow {OC'} = 2\overrightarrow {OC} ;\,\overrightarrow {OD'} = 2\overrightarrow {OD} \).
Từ đó ta có các điểm A', B', C', D' lần lượt là ảnh của các điểm A, B, C, D qua phép vị tự \({V_{\left( {O,2} \right)}}\). Do đó, phép vị tự V(O, 2) biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.
Vậy phép vị tự \({V_{\left( {O,2} \right)}}\) biến bức tranh nhỏ thành bức tranh lớn. Khi đó, phép vị tự \({V_{\left( {O,\frac{1}{2}} \right)}}\) biến bức tranh lớn thành bức tranh nhỏ.
- Hoạt động 1
- Câu hỏi
- Luyện tập 1
- Vận dụng 1
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Hãy tính các tỉ số \(\frac{{OA}}{{OA'}},\,\frac{{OB}}{{OB'}},\,\frac{{OC}}{{OC'}},\,\frac{{OD}}{{OD'}}\).
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Phương pháp giải:
Dựa vào định lí Thalès để chứng minh A, B, C, D lần lượt là trung điểm của A’O, B’O, C’O, D’O.
Lời giải chi tiết:
a) Gọi O là giao điểm của AA' và BB'.
Xét tam giác OA'B' có AB // A'B', theo định lý Thales, ta có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\)
Từ đó suy ra A, B lần lượt là trung điểm của OA' và OB'.
Gọi C" là giao điểm của BC và OC'. Vì BC // B'C' nên BC" // B'C'.
Xét tam giác OB'C' có BC" // B'C' và B là trung điểm của OB' nên BC" là đường trung bình của tam giác OB'C'. Suy ra và C" là trung điểm của OC'.
Mặt khác theo giả thiết ta có \(BC = \frac{1}{2}B'C'\). Do vậy C" trùng với C và C là trung điểm của OC'.
Chứng minh tương tự, ta được D là trung điểm của OD'.
Vậy các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Vì A, B, C, D lần lượt là trung điểm của OA', OB', OC', OD' nên
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\).
c) Dùng thước thẳng nối hai điểm tương ứng trên hai bức tranh, cụ thể, đầu mỏ trên của chú gà ở hai bức tranh, ta thấy đường thẳng này đi qua điểm O.
Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm nào? Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm nào?
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
- Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm O.
- Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm M.
Thật vậy, nếu M' là ảnh M qua phép vị tự \({V_{(O,{\rm{ }}k)}}\) thì \(\overrightarrow {OM'} = k\overrightarrow {OM} \Leftrightarrow \overrightarrow {OM} = \frac{1}{k}\overrightarrow {OM'} \). Điều này có nghĩa là M là ảnh của M' qua phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\).
Chứng minh rằng, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất, phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
+ Phép vị tự \({V_{(O,{\rm{ }}1)}}\) biến điểm M thành điểm M' thỏa mãn \(\overrightarrow {OM'} = \overrightarrow {OM} \). Khi đó M' trùng với M. Do đó, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất.
+ Phép vị tự \({V_{\left( {o,-1} \right)}}\;\) biến điểm M thành điểm M" thỏa mãn . Khi đó O là trung điểm của MM". Do đó, M" là ảnh của M qua phép đối xứng tâm O hay phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.
Phương pháp giải:
Quan sát hình ảnh và tìm tỉ số k
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
Ta có: \(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{OD}}{{OD'}} = \frac{1}{2}\) (theo HĐ1).
Suy ra \(\overrightarrow {OA'} = 2\overrightarrow {OA} ;\,\overrightarrow {OB'} = 2\overrightarrow {OB} ;\,\overrightarrow {OC'} = 2\overrightarrow {OC} ;\,\overrightarrow {OD'} = 2\overrightarrow {OD} \).
Từ đó ta có các điểm A', B', C', D' lần lượt là ảnh của các điểm A, B, C, D qua phép vị tự \({V_{\left( {O,2} \right)}}\). Do đó, phép vị tự V(O, 2) biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.
Vậy phép vị tự \({V_{\left( {O,2} \right)}}\) biến bức tranh nhỏ thành bức tranh lớn. Khi đó, phép vị tự \({V_{\left( {O,\frac{1}{2}} \right)}}\) biến bức tranh lớn thành bức tranh nhỏ.
Giải mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 26, 27 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và áp dụng linh hoạt các công thức, định lý đã học. Để giúp các em học sinh giải quyết các bài tập một cách hiệu quả, tusach.vn xin trình bày chi tiết lời giải cho từng bài tập trong mục này.
Nội dung chính của Mục 1 trang 26, 27
Thông thường, mục này sẽ xoay quanh các chủ đề như:
- Đạo hàm của hàm số lượng giác: Tính đạo hàm của sinx, cosx, tanx, cotx và các hàm hợp.
- Ứng dụng đạo hàm trong việc khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị của hàm số lượng giác.
- Bài toán thực tế liên quan đến đạo hàm: Giải các bài toán về vận tốc, gia tốc, tối ưu hóa.
Hướng dẫn giải chi tiết từng bài tập
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 26, 27:
Bài 1: (Ví dụ minh họa)
Đề bài: Tính đạo hàm của hàm số y = sin(2x + 1).
Lời giải:
- Sử dụng công thức đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x)
- Đặt u(t) = sin(t) và v(x) = 2x + 1
- Khi đó, u'(t) = cos(t) và v'(x) = 2
- Vậy, y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Bài 2: (Ví dụ minh họa)
Đề bài: Tìm cực trị của hàm số y = x + cos(x).
Lời giải:
- Tính đạo hàm bậc nhất: y' = 1 - sin(x)
- Giải phương trình y' = 0: 1 - sin(x) = 0 => sin(x) = 1 => x = π/2 + kπ (k ∈ Z)
- Tính đạo hàm bậc hai: y'' = -cos(x)
- Xét dấu y'' tại các điểm cực trị:
- Khi x = π/2 + 2kπ: y'' = -cos(π/2 + 2kπ) = 0 (Không đủ điều kiện để xác định cực trị)
- Khi x = 3π/2 + 2kπ: y'' = -cos(3π/2 + 2kπ) = 0 (Không đủ điều kiện để xác định cực trị)
- Kết luận: Hàm số không có cực trị.
Mẹo giải nhanh và hiệu quả
Để giải các bài tập về đạo hàm hàm số lượng giác một cách nhanh chóng và hiệu quả, các em cần:
- Nắm vững các công thức đạo hàm cơ bản của các hàm số lượng giác.
- Thành thạo công thức đạo hàm của hàm hợp.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.
Tài liệu tham khảo thêm
Ngoài sách giáo khoa và chuyên đề học tập, các em có thể tham khảo thêm các tài liệu sau:
- Các bài giảng trực tuyến về đạo hàm.
- Các trang web học toán uy tín.
- Các video hướng dẫn giải bài tập toán.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thức. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!