Giải bài 1.33 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài 1.33 thuộc chương trình Chuyên đề học tập Toán 11 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
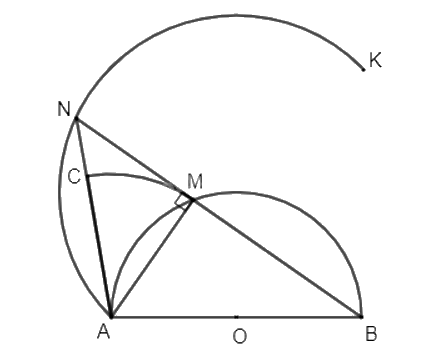
Cho nửa đường tròn tâm O, đường kính AB và điểm M trên nửa đường tròn đó.
Giải bài 1.33 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu
Bài 1.33 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là hướng dẫn giải chi tiết bài tập này, giúp các em hiểu rõ phương pháp và tự tin giải các bài tập tương tự.
Nội dung bài tập 1.33 trang 33
Bài 1.33 yêu cầu học sinh sử dụng kiến thức về đạo hàm để tìm điểm cực trị của hàm số. Cụ thể, bài tập thường cho một hàm số và yêu cầu tìm:
- Các điểm cực đại, cực tiểu của hàm số.
- Giá trị cực đại, giá trị cực tiểu của hàm số.
Phương pháp giải bài tập 1.33
Để giải bài tập 1.33, các em cần thực hiện các bước sau:
- Tính đạo hàm cấp một (f'(x)) của hàm số.
- Tìm các điểm dừng của hàm số bằng cách giải phương trình f'(x) = 0.
- Lập bảng xét dấu f'(x) để xác định khoảng đồng biến, nghịch biến của hàm số.
- Kết luận về điểm cực đại, cực tiểu dựa vào bảng xét dấu f'(x).
- Tính giá trị cực đại, cực tiểu bằng cách thay giá trị x của điểm cực đại, cực tiểu vào hàm số ban đầu.
Ví dụ minh họa giải bài 1.33 trang 33
Giả sử hàm số cho là: f(x) = x3 - 3x2 + 2
- Tính đạo hàm cấp một: f'(x) = 3x2 - 6x
- Tìm điểm dừng: 3x2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
- Lập bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
- Kết luận:
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu ý khi giải bài tập 1.33
- Đảm bảo tính chính xác khi tính đạo hàm.
- Lập bảng xét dấu f'(x) một cách cẩn thận để tránh sai sót.
- Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín
tusach.vn là website cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm giải bài tập, lý thuyết, đề thi và các bài giảng online. Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo tính chính xác, dễ hiểu cho học sinh. Hãy truy cập tusach.vn để học tập hiệu quả và đạt kết quả cao trong môn Toán!