Giải mục 2 trang 43, 44 Chuyên đề học tập Toán 11 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 43, 44 Chuyên đề học tập Toán 11 - Kết nối tri thức trên tusach.vn.
Chúng tôi hiểu rằng việc tự học và làm bài tập có thể gặp nhiều khó khăn. Do đó, đội ngũ giáo viên giàu kinh nghiệm của tusach.vn đã biên soạn lời giải bài tập một cách cẩn thận, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
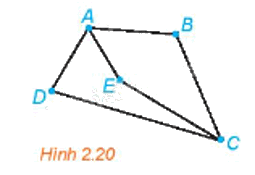
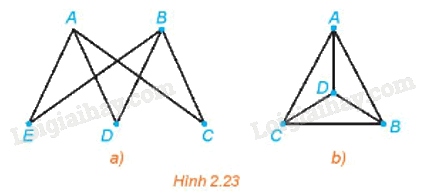
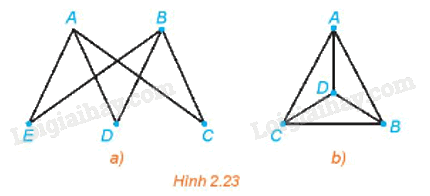
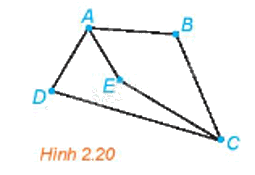
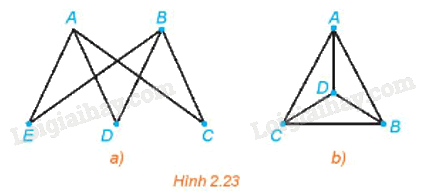
Có 5 thành phố du lịch A, B, C, D, E và các con đường nối các thành phố này như Hình 2.20
Giải mục 2 trang 43, 44 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 2 trang 43, 44 trong Chuyên đề học tập Toán 11 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Đây là một phần quan trọng trong chương trình Toán 11, đóng vai trò nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục này, cùng với những lưu ý quan trọng để giúp các em hiểu rõ hơn về các khái niệm và kỹ năng liên quan.
Nội dung chính của Mục 2
- Ôn tập khái niệm đạo hàm: Nhắc lại định nghĩa đạo hàm, ý nghĩa hình học và vật lý của đạo hàm.
- Các quy tắc tính đạo hàm: Tổng hợp các quy tắc tính đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số lượng giác: Công thức đạo hàm của sinx, cosx, tanx, cotx.
- Bài tập áp dụng: Các bài tập vận dụng các kiến thức trên để tính đạo hàm của các hàm số khác nhau.
Giải chi tiết bài tập 1 (trang 43)
Đề bài: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Lời giải:
- Áp dụng quy tắc đạo hàm của tổng: f'(x) = (3x2)' + (2x)' + (-1)'
- Áp dụng quy tắc đạo hàm của lũy thừa: (3x2)' = 6x, (2x)' = 2
- Đạo hàm của hằng số bằng 0: (-1)' = 0
- Vậy, f'(x) = 6x + 2
Giải chi tiết bài tập 2 (trang 44)
Đề bài: Tính đạo hàm của hàm số g(x) = sinx + cosx.
Lời giải:
- Áp dụng quy tắc đạo hàm của tổng: g'(x) = (sinx)' + (cosx)'
- Áp dụng công thức đạo hàm của sinx và cosx: (sinx)' = cosx, (cosx)' = -sinx
- Vậy, g'(x) = cosx - sinx
Lưu ý quan trọng khi giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Kiểm tra lại kết quả sau khi tính đạo hàm.
- Sử dụng máy tính cầm tay để kiểm tra kết quả (nếu cần thiết).
Bảng tổng hợp công thức đạo hàm thường dùng
| Hàm số | Đạo hàm |
|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sinx | f'(x) = cosx |
| f(x) = cosx | f'(x) = -sinx |
Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi giải các bài tập về đạo hàm trong Chuyên đề học tập Toán 11 - Kết nối tri thức. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi trong phần bình luận bên dưới. Chúc các em học tốt!
Tusach.vn - Đồng hành cùng các em trên con đường chinh phục tri thức.