Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng Tusach.vn khám phá lời giải bài 3.21 này nhé!
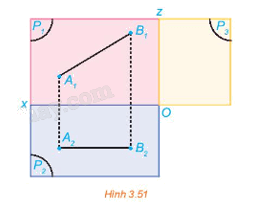
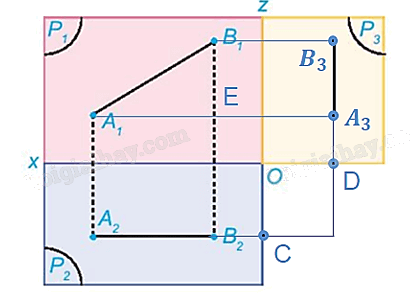
Hình 3.51 thể hiện hình chiếu đứng và hình chiếu bằng của một đoạn thẳng AB trong không gian.
Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức: Đề bài
Bài 3.21 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Cụ thể, đề bài có thể yêu cầu:
- Xác định tập xác định của hàm số.
- Tính đạo hàm bậc nhất và bậc hai của hàm số.
- Tìm các điểm cực trị của hàm số (cực đại, cực tiểu).
- Khảo sát tính đơn điệu của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết bài 3.21 trang 80
Để giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức, chúng ta sẽ thực hiện các bước sau:
- Bước 1: Xác định tập xác định của hàm số. Tập xác định là tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
- Bước 2: Tính đạo hàm bậc nhất. Sử dụng các quy tắc đạo hàm cơ bản để tính đạo hàm f'(x).
- Bước 3: Tìm các điểm cực trị. Giải phương trình f'(x) = 0 để tìm các điểm nghiệm. Sau đó, xét dấu của f'(x) để xác định loại điểm cực trị (cực đại hoặc cực tiểu).
- Bước 4: Tính đạo hàm bậc hai. Sử dụng các quy tắc đạo hàm để tính đạo hàm f''(x).
- Bước 5: Khảo sát tính lồi, lõm của hàm số. Xét dấu của f''(x) để xác định khoảng hàm số lồi và lõm.
- Bước 6: Tìm điểm uốn. Giải phương trình f''(x) = 0 để tìm các điểm uốn.
- Bước 7: Vẽ đồ thị hàm số. Dựa vào các thông tin đã thu thập được, vẽ đồ thị hàm số.
Ví dụ minh họa
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước trên để giải bài toán.
Bước 1: Tập xác định của hàm số là R.
Bước 2: f'(x) = 3x2 - 6x.
Bước 3: Giải phương trình 3x2 - 6x = 0, ta được x = 0 và x = 2. Xét dấu của f'(x), ta thấy:
- Khi x < 0, f'(x) > 0, hàm số đồng biến.
- Khi 0 < x < 2, f'(x) < 0, hàm số nghịch biến.
- Khi x > 2, f'(x) > 0, hàm số đồng biến.
Vậy hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Bước 4: f''(x) = 6x - 6.
Bước 5: Giải phương trình 6x - 6 = 0, ta được x = 1. Xét dấu của f''(x), ta thấy:
- Khi x < 1, f''(x) < 0, hàm số lõm.
- Khi x > 1, f''(x) > 0, hàm số lồi.
Vậy hàm số có điểm uốn tại x = 1.
Lưu ý khi giải bài tập
- Nắm vững các quy tắc đạo hàm cơ bản.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn - Đồng hành cùng bạn học Toán
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập Toán 11 Kết nối tri thức. Hãy truy cập Tusach.vn để học Toán hiệu quả hơn!