Giải mục 1 trang 12, 13 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 12, 13 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 12, 13 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất, hỗ trợ học sinh học tập hiệu quả và đạt kết quả tốt nhất.
Cầu Ponte Sisto in hình dưới dòng sông Tiber, tạo nên một hình ảnh có tính đối xứng trục
Luyện tập 1
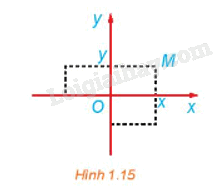
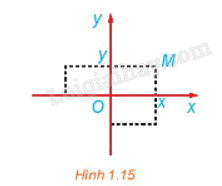
Xét mặt phẳng tọa độ Oxy (H.1.15). Trong các khẳng định sau, chọn các khẳng định đúng.
a) Phép đối xứng trục Ox biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\)thành điểm có tọa độ \(\left( {x;{\rm{ }}-{\rm{ }}y} \right).\)
b) Phép đối xứng trục Oy biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\)thành điểm có tọa độ \(\left( {-{\rm{ }}x;{\rm{ }}y} \right).\)
c) Phép đối xứng trục Ox biến A(1; 2) thành điểm \(A'\left( {-{\rm{ }}1;{\rm{ }}-{\rm{ }}2} \right).\)
Phương pháp giải:
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết:
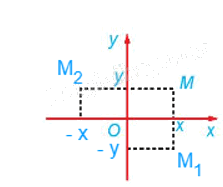
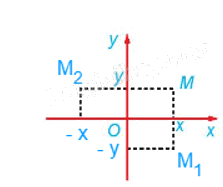
Từ hình vẽ ta thấy:
+) Phép đối xứng trục Ox biến mỗi điểm M(x; y) thành điểm M1(x; – y).
+) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm M2(– x; y).
Do đó, phép đối xứng trục Ox biến điểm A(1; 2) thành A'(1; – 2).
Vậy các khẳng định a), b) đúng và khẳng định c) sai.
Hoạt động 1
Cầu Ponte Sisto in hình dưới dòng sông Tiber, tạo nên một hình ảnh có tính đối xứng trục.

a) Hãy chỉ ra trục đối xứng của hình ảnh đó.
b) Có thể đếm được bao nhiêu hình bóng điện dưới sông? Mỗi hình đó là ảnh dưới sông của bóng điện nào trên cầu?
Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
a) Đường thẳng giao bởi cầu và mặt nước trên dòng sông là trục đối xứng của hình ảnh đó (đường màu xanh trong hình vẽ).

b) Có thể đếm được 5 bóng điện dưới dòng sông. Mỗi hình đó là ảnh dưới sông của bóng điện tương ứng với từng số thứ tự trên cầu như ảnh.

- Hoạt động 1
- Luyện tập 1
Cầu Ponte Sisto in hình dưới dòng sông Tiber, tạo nên một hình ảnh có tính đối xứng trục.
a) Hãy chỉ ra trục đối xứng của hình ảnh đó.
b) Có thể đếm được bao nhiêu hình bóng điện dưới sông? Mỗi hình đó là ảnh dưới sông của bóng điện nào trên cầu?
Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
a) Đường thẳng giao bởi cầu và mặt nước trên dòng sông là trục đối xứng của hình ảnh đó (đường màu xanh trong hình vẽ).
b) Có thể đếm được 5 bóng điện dưới dòng sông. Mỗi hình đó là ảnh dưới sông của bóng điện tương ứng với từng số thứ tự trên cầu như ảnh.

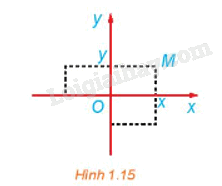
Xét mặt phẳng tọa độ Oxy (H.1.15). Trong các khẳng định sau, chọn các khẳng định đúng.
a) Phép đối xứng trục Ox biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\)thành điểm có tọa độ \(\left( {x;{\rm{ }}-{\rm{ }}y} \right).\)
b) Phép đối xứng trục Oy biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\)thành điểm có tọa độ \(\left( {-{\rm{ }}x;{\rm{ }}y} \right).\)
c) Phép đối xứng trục Ox biến A(1; 2) thành điểm \(A'\left( {-{\rm{ }}1;{\rm{ }}-{\rm{ }}2} \right).\)
Phương pháp giải:
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết:
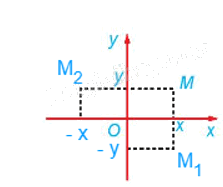
Từ hình vẽ ta thấy:
+) Phép đối xứng trục Ox biến mỗi điểm M(x; y) thành điểm M1(x; – y).
+) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm M2(– x; y).
Do đó, phép đối xứng trục Ox biến điểm A(1; 2) thành A'(1; – 2).
Vậy các khẳng định a), b) đúng và khẳng định c) sai.
Giải mục 1 trang 12, 13 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Chuyên đề học tập Toán 11 - Kết nối tri thức là một phần quan trọng trong chương trình học Toán lớp 11. Mục 1 trang 12, 13 tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai, bao gồm các khái niệm, tính chất, và phương pháp giải các bài toán liên quan. Việc nắm vững kiến thức này là nền tảng để học tốt các chuyên đề tiếp theo.
Nội dung chính của Mục 1 trang 12, 13
- Ôn tập về hàm số bậc hai: Định nghĩa, dạng tổng quát, đồ thị, các yếu tố của đồ thị (đỉnh, trục đối xứng, giao điểm với các trục tọa độ).
- Các dạng bài tập thường gặp: Xác định các hệ số của hàm số bậc hai, tìm đỉnh của parabol, tìm giao điểm của parabol với đường thẳng, giải phương trình bậc hai.
- Ứng dụng của hàm số bậc hai: Giải các bài toán thực tế liên quan đến quỹ đạo của vật thể, tối ưu hóa diện tích, thể tích.
Hướng dẫn giải chi tiết các bài tập trong Mục 1
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 1 trang 12, 13 Chuyên đề học tập Toán 11 - Kết nối tri thức:
Bài 1: Xác định các hệ số a, b, c của hàm số y = 2x2 - 5x + 3
Lời giải: Hàm số y = 2x2 - 5x + 3 có dạng y = ax2 + bx + c. So sánh với dạng tổng quát, ta có a = 2, b = -5, c = 3.
Bài 2: Tìm đỉnh của parabol y = x2 - 4x + 3
Lời giải: Hoành độ đỉnh của parabol là x = -b / 2a = -(-4) / (2 * 1) = 2. Tung độ đỉnh là y = (2)2 - 4 * 2 + 3 = -1. Vậy đỉnh của parabol là (2, -1).
Bài 3: Giải phương trình x2 - 5x + 6 = 0
Lời giải: Phương trình x2 - 5x + 6 = 0 có a = 1, b = -5, c = 6. Tính delta: Δ = b2 - 4ac = (-5)2 - 4 * 1 * 6 = 1. Vì Δ > 0, phương trình có hai nghiệm phân biệt:
- x1 = (-b + √Δ) / 2a = (5 + 1) / 2 = 3
- x2 = (-b - √Δ) / 2a = (5 - 1) / 2 = 2
Vậy phương trình có hai nghiệm là x1 = 3 và x2 = 2.
Mẹo học tập hiệu quả
- Nắm vững định nghĩa và tính chất: Hiểu rõ các khái niệm cơ bản về hàm số bậc hai, đồ thị, và các yếu tố của đồ thị.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
- Sử dụng các công cụ hỗ trợ: Sử dụng máy tính bỏ túi, phần mềm vẽ đồ thị, hoặc các trang web học tập trực tuyến để kiểm tra và củng cố kiến thức.
- Hỏi thầy cô hoặc bạn bè: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô hoặc bạn bè để được giúp đỡ.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn cam kết cung cấp những tài liệu học tập chất lượng, chính xác và dễ hiểu. Chúng tôi luôn cập nhật những thông tin mới nhất và hỗ trợ học sinh học tập hiệu quả. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chủ đề | Nội dung |
|---|---|
| Hàm số bậc hai | Định nghĩa, dạng tổng quát, đồ thị |
| Bài tập ứng dụng | Giải phương trình, tìm đỉnh, ứng dụng thực tế |
| Tusach.vn - Nguồn tài liệu học tập uy tín | |