Giải bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng quan nội dung
Giải bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng Tusach.vn khám phá lời giải bài 3.11 trang 66 ngay dưới đây!
Hình chiếu trục đo của một vật thể được vẽ trên giấy kẻ ô tam giác đều như trong Hình 3.31.
Đề bài
Hình chiếu trục đo của một vật thể được vẽ trên giấy kẻ ô tam giác đều như trong Hình 3.31. Quy ước độ dài mỗi cạnh của tam giác đều là 10 cm, tính thể tích của vật thể đó.
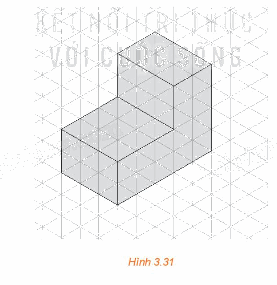
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ để trả lời
Lời giải chi tiết
Chia vật thể thành hai hình hộp chữ nhật A và B (hình vẽ dưới).
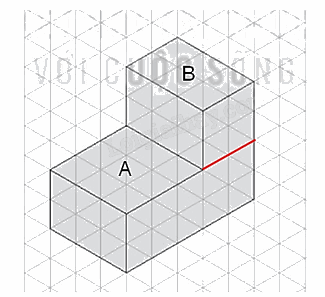
Hình hộp chữ nhật A có: Chiều dài đáy 50 cm, chiều rộng đáy 30 cm, chiều cao 20 cm.
Thể tích hình hộp chữ nhật A là: 50 . 30 . 20 = 30 000 (cm3).
Hình hộp chữ nhật B có: Chiều dài đáy 30 cm, chiều rộng đáy 20 cm, chiều cao 20 cm.
Thể tích hình hộp chữ nhật B là: 30 . 20 . 20 = 12 000 (cm3).
Do đó, thể tích vật thể là: 30 000 + 12 000 = 42 000 (cm3).
Giải bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài này, chúng ta cần nắm vững các bước sau:
- Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
- Tính đạo hàm bậc nhất: Sử dụng các quy tắc đạo hàm để tìm f'(x).
- Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0.
- Lập bảng biến thiên: Xác định dấu của f'(x) trên các khoảng xác định bởi các điểm dừng để xác định khoảng hàm số đồng biến, nghịch biến.
- Kết luận về cực trị: Dựa vào bảng biến thiên để xác định các điểm cực đại, cực tiểu của hàm số.
Lời giải chi tiết bài 3.11 trang 66
Đề bài: (Giả sử đề bài cụ thể của bài 3.11 được đưa ra ở đây. Ví dụ: Khảo sát hàm số y = x3 - 3x2 + 2)
Giải:
- Tập xác định: Hàm số y = x3 - 3x2 + 2 có tập xác định là D = ℝ.
- Đạo hàm bậc nhất: y' = 3x2 - 6x.
- Điểm dừng: Giải phương trình 3x2 - 6x = 0, ta được x = 0 hoặc x = 2.
- Bảng biến thiên:
x -∞ 0 2 +∞ y' + - + y ↗ ↘ ↗ - Kết luận: Hàm số đạt cực đại tại x = 0, yCĐ = 2 và đạt cực tiểu tại x = 2, yCT = -2.
Lưu ý quan trọng khi giải bài tập về khảo sát hàm số
- Luôn kiểm tra kỹ tập xác định của hàm số.
- Tính đạo hàm chính xác và cẩn thận.
- Lập bảng biến thiên một cách khoa học và rõ ràng.
- Kết luận về cực trị dựa trên bảng biến thiên.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức. Chúng tôi hy vọng rằng với những hướng dẫn này, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.
Ngoài ra, các em có thể tham khảo thêm các bài giải khác tại tusach.vn.