Giải mục 2 trang 17, 18 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 17, 18 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 17, 18 trong Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ các khái niệm, công thức và phương pháp giải bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em.
Khi mặt bàn ăn quay, mặc dù các đĩa thức ăn trên bàn đều dịch chuyển tới vị trí mới nhưng khoảng cách giữa hai đĩa thức ăn có bị thay đổi hay không?
Hoạt động 2
Khi mặt bàn ăn quay, mặc dù các đĩa thức ăn trên bàn đều dịch chuyển tới vị trí mới nhưng khoảng cách giữa hai đĩa thức ăn có bị thay đổi hay không?
Phương pháp giải:
Suy luận thực tiễn để trả lời
Lời giải chi tiết:
Khoảng cách giữa hai đĩa thức ăn không bị thay đổi khi mặt bàn ăn quay.
Vận dụng 1
Trong tình huống mở đầu, mặt bàn tròn đặt đồ ăn được thiết kế để có thể quay quanh tâm mặt bàn. Coi mặt bàn tròn là hình tròn tâm O, bán kính R. Hỏi, khi thực hiện phép quay tâm O với góc quay \(\alpha \) bất kì thì:
- Điểm O biến thành điểm nào?
- Đường tròn (O, R) biến thành đường tròn nào?
- Vị trí của mặt bàn có bị dịch chuyển hay không?
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết:
Điểm O là tâm quay nên khi thực hiện phép quay tâm O với góc quay α bất kì thì điểm O biến thành điểm O, đường tròn (O; R) biến thành đường tròn (O; R).
Vậy vị trí của mặt bàn không bị dịch chuyển.
Luyện tập 2
Trong Hình 1.26, ABCDEF là lục giác đều có tâm O. Tìm ảnh của tam giác ACE qua các phép quay \({Q_{\left( {O,\,\frac{\pi }{3}} \right)}},\,\,{Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\)
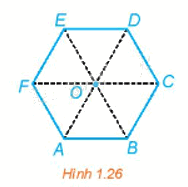
Phương pháp giải:
Phép quay tâm O, góc quay :
Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Lời giải chi tiết:
Ta có: ABCDEF là lục giác đều nên
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = 60^\circ = \frac{\pi }{3}\) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC{\rm{ }} = {\rm{ }}OD{\rm{ }} = {\rm{ }}OE{\rm{ }} = {\rm{ }}OF\).
Do đó, phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến các điểm A, C, E tương ứng thành các điểm B, D, F.
Vậy phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến tam giác ACE thành tam giác BDF.
Ta có: \(\widehat {AOE} = \widehat {AOF} + \widehat {EOF} = \frac{{2\pi }}{3}\), tương tự \(\widehat {COA} = \widehat {EOC} = \frac{{2\pi }}{3}\)
Vì OA = OE và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm A thành điểm E.
Vì OC = OA và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm C thành điểm A.
Vì OE = OC và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm E thành điểm C.
Vậy phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến tam giác ACE thành tam giác ECA hay biến tam giác ACE thành chính nó.
- Hoạt động 2
- Luyện tập 2
- Vận dụng 1
Khi mặt bàn ăn quay, mặc dù các đĩa thức ăn trên bàn đều dịch chuyển tới vị trí mới nhưng khoảng cách giữa hai đĩa thức ăn có bị thay đổi hay không?
Phương pháp giải:
Suy luận thực tiễn để trả lời
Lời giải chi tiết:
Khoảng cách giữa hai đĩa thức ăn không bị thay đổi khi mặt bàn ăn quay.
Trong Hình 1.26, ABCDEF là lục giác đều có tâm O. Tìm ảnh của tam giác ACE qua các phép quay \({Q_{\left( {O,\,\frac{\pi }{3}} \right)}},\,\,{Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\)
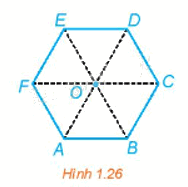
Phương pháp giải:
Phép quay tâm O, góc quay :
Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Lời giải chi tiết:
Ta có: ABCDEF là lục giác đều nên
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = 60^\circ = \frac{\pi }{3}\) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC{\rm{ }} = {\rm{ }}OD{\rm{ }} = {\rm{ }}OE{\rm{ }} = {\rm{ }}OF\).
Do đó, phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến các điểm A, C, E tương ứng thành các điểm B, D, F.
Vậy phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến tam giác ACE thành tam giác BDF.
Ta có: \(\widehat {AOE} = \widehat {AOF} + \widehat {EOF} = \frac{{2\pi }}{3}\), tương tự \(\widehat {COA} = \widehat {EOC} = \frac{{2\pi }}{3}\)
Vì OA = OE và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm A thành điểm E.
Vì OC = OA và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm C thành điểm A.
Vì OE = OC và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm E thành điểm C.
Vậy phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến tam giác ACE thành tam giác ECA hay biến tam giác ACE thành chính nó.
Trong tình huống mở đầu, mặt bàn tròn đặt đồ ăn được thiết kế để có thể quay quanh tâm mặt bàn. Coi mặt bàn tròn là hình tròn tâm O, bán kính R. Hỏi, khi thực hiện phép quay tâm O với góc quay \(\alpha \) bất kì thì:
- Điểm O biến thành điểm nào?
- Đường tròn (O, R) biến thành đường tròn nào?
- Vị trí của mặt bàn có bị dịch chuyển hay không?
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết:
Điểm O là tâm quay nên khi thực hiện phép quay tâm O với góc quay α bất kì thì điểm O biến thành điểm O, đường tròn (O; R) biến thành đường tròn (O; R).
Vậy vị trí của mặt bàn không bị dịch chuyển.
Giải mục 2 trang 17, 18 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và hướng dẫn chi tiết
Mục 2 trang 17, 18 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, ví dụ như các dạng bài tập về hàm số, phương trình, bất phương trình, hoặc các bài toán liên quan đến hình học. Việc nắm vững kiến thức và kỹ năng giải các bài tập trong mục này là rất quan trọng để các em học sinh có thể tự tin làm bài kiểm tra và thi cử.
Nội dung chính của Mục 2 trang 17, 18
Để hiểu rõ hơn về nội dung của Mục 2, chúng ta cần xem xét các phần sau:
- Lý thuyết trọng tâm: Tóm tắt các định nghĩa, định lý, công thức quan trọng liên quan đến chủ đề đang học.
- Ví dụ minh họa: Các bài toán được giải chi tiết để giúp các em hiểu rõ cách áp dụng lý thuyết vào thực tế.
- Bài tập luyện tập: Các bài tập với mức độ khó tăng dần để các em có thể rèn luyện kỹ năng giải toán.
Hướng dẫn giải chi tiết các bài tập trong Mục 2
Dưới đây là hướng dẫn giải chi tiết một số bài tập thường gặp trong Mục 2 trang 17, 18:
Bài tập 1: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng)
Bài tập 2: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng)
Các dạng bài tập thường gặp và phương pháp giải
Mục 2 thường bao gồm các dạng bài tập sau:
- Dạng 1: Bài tập về... (Mô tả dạng bài và phương pháp giải)
- Dạng 2: Bài tập về... (Mô tả dạng bài và phương pháp giải)
- Dạng 3: Bài tập về... (Mô tả dạng bài và phương pháp giải)
Mẹo giải nhanh và tránh sai lầm
Để giải các bài tập trong Mục 2 một cách nhanh chóng và chính xác, các em có thể tham khảo một số mẹo sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
- Sử dụng các công thức và định lý một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Tài liệu tham khảo thêm
Ngoài sách giáo khoa và Chuyên đề học tập, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11
- Các trang web học toán trực tuyến
- Các video hướng dẫn giải toán trên YouTube
Tusach.vn hy vọng rằng với những hướng dẫn chi tiết và hữu ích này, các em học sinh sẽ có thể tự tin giải các bài tập trong Mục 2 trang 17, 18 Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúc các em học tập tốt!
| Chủ đề | Nội dung chính |
|---|---|
| Hàm số | Định nghĩa, tính chất, đồ thị... |
| Phương trình | Các loại phương trình, phương pháp giải... |