Giải bài 2.12 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng quan nội dung
Giải bài 2.12 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài tập 2.12 trang 45 trong Chuyên đề học tập Toán 11 Kết nối tri thức. Chúng tôi sẽ trình bày các bước giải một cách rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán!
a) Giả sử G là một đồ thị với n đỉnh và (frac{{left( {n - 1} right)left( {n - 2} right)}}{2} + 2) cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.
Đề bài
a) Giả sử G là một đồ thị với n đỉnh và \(\frac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2} + 2\) cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.
b) Tìm một đồ thị với n đỉnh và \(\frac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2} + 1\) cạnh mà không có chu trình Hamilton.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức vừa học để làm
Lời giải chi tiết
a) Định lí Ore: Nếu G là một đồ thị có n đỉnh \(\left( {n \ge 3} \right)\) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.
Ta có lí thuyết: Giả sử G là đồ thị đơn gồm n đỉnh và m cạnh. Nếu \(m \ge \;\frac{{{n^2} - 3n\; + 6}}{2}\) thì G là đồ thị có chu trình Hamilton.
Áp dụng vào bài toán ta được điều phải chứng minh.
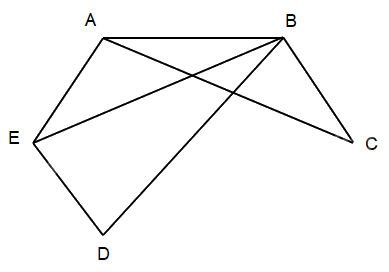
b) Ta có đồ thị sau có 5 đỉnh, 7 cạnh và đồ thị không có chu trình Hamilton.
Giải bài 2.12 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 2.12 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Đề bài:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M là trung điểm của CD. Biết SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SM và mặt phẳng (ABCD).
Lời giải:
- Xác định các yếu tố cần thiết:
- Đáy ABCD là hình vuông cạnh a.
- SA vuông góc với (ABCD) và SA = a.
- M là trung điểm của CD.
- Vẽ hình:
Vẽ hình chóp S.ABCD và các đường thẳng, mặt phẳng liên quan đến bài toán. Việc vẽ hình chính xác sẽ giúp chúng ta hình dung rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
- Tìm góc giữa SM và mặt phẳng (ABCD):
Vì SA vuông góc với (ABCD) nên góc giữa SM và mặt phẳng (ABCD) chính là góc giữa SM và hình chiếu của SM lên mặt phẳng (ABCD), tức là góc SMA.
- Tính góc SMA:
Trong tam giác vuông SAM, ta có:
- SA = a
- AM = a√2 / 2 (vì M là trung điểm của CD và ABCD là hình vuông)
Do đó, tan SMA = SA / AM = a / (a√2 / 2) = √2.
Suy ra, SMA = arctan(√2) ≈ 54.74°.
Kết luận:
Góc giữa đường thẳng SM và mặt phẳng (ABCD) là arctan(√2) ≈ 54.74°.
Các lưu ý khi giải bài tập:
- Nắm vững các khái niệm cơ bản về đường thẳng và mặt phẳng trong không gian.
- Sử dụng các định lý liên quan một cách linh hoạt.
- Vẽ hình chính xác để hình dung rõ hơn về bài toán.
- Kiểm tra lại kết quả sau khi giải xong.
Bài tập tương tự:
Để củng cố kiến thức, bạn có thể giải các bài tập tương tự trong sách giáo khoa và sách bài tập. Tusach.vn sẽ tiếp tục cập nhật lời giải cho các bài tập khác trong Chuyên đề học tập Toán 11 Kết nối tri thức.
Tusach.vn - Đồng hành cùng bạn học Toán!
Chúng tôi hy vọng bài giải này sẽ giúp bạn hiểu rõ hơn về bài tập 2.12 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức. Hãy truy cập tusach.vn để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.