Giải mục 2 trang 37, 38 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 37, 38 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 37, 38 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của các em.
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
Luyện tập 4
Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Giả sử có đồ thị thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.
Khi đó, ta có số đỉnh bậc 4 là: \(12{\rm{ }}-{\rm{ }}x.\)
Tổng số bậc của các đỉnh là: \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right).\)
Vì đồ thị có 28 cạnh nên theo Định lí bắt tay thì đồ thị có tổng số bậc là \(28{\rm{ }}.{\rm{ }}2{\rm{ }} = {\rm{ }}56.\)
Do đó, ta có phương trình \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right){\rm{ }} = {\rm{ }}56\), tức là \(8{\rm{ }} + {\rm{ }}x{\rm{ }} = {\rm{ }}0\). Phương trình này không có nghiệm là số tự nhiên, do đó không tồn tại đồ thị thỏa mãn điều kiện đề bài.
- Hoạt động 4
- Luyện tập 4
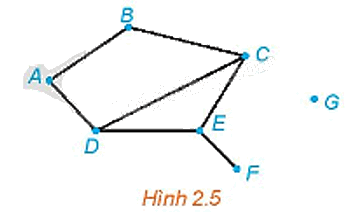
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
Phương pháp giải:
Dựa vào hình 2.5 để làm
Lời giải chi tiết:
Đỉnh là đầu mút của 0 cạnh là đỉnh G.
Đỉnh là đầu mút của 1 cạnh là đỉnh F.
Các đỉnh là đầu mút của 2 cạnh là các đỉnh A, B.
Các đỉnh là đầu mút của 3 cạnh là các đỉnh C, D, E.
Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Giả sử có đồ thị thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.
Khi đó, ta có số đỉnh bậc 4 là: \(12{\rm{ }}-{\rm{ }}x.\)
Tổng số bậc của các đỉnh là: \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right).\)
Vì đồ thị có 28 cạnh nên theo Định lí bắt tay thì đồ thị có tổng số bậc là \(28{\rm{ }}.{\rm{ }}2{\rm{ }} = {\rm{ }}56.\)
Do đó, ta có phương trình \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right){\rm{ }} = {\rm{ }}56\), tức là \(8{\rm{ }} + {\rm{ }}x{\rm{ }} = {\rm{ }}0\). Phương trình này không có nghiệm là số tự nhiên, do đó không tồn tại đồ thị thỏa mãn điều kiện đề bài.
Hoạt động 4
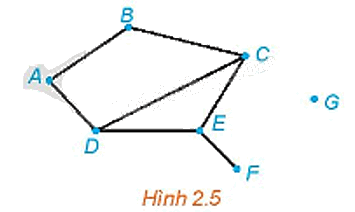
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
Phương pháp giải:
Dựa vào hình 2.5 để làm
Lời giải chi tiết:
Đỉnh là đầu mút của 0 cạnh là đỉnh G.
Đỉnh là đầu mút của 1 cạnh là đỉnh F.
Các đỉnh là đầu mút của 2 cạnh là các đỉnh A, B.
Các đỉnh là đầu mút của 3 cạnh là các đỉnh C, D, E.
Giải mục 2 trang 37, 38 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 2 trang 37, 38 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Để giải quyết các bài tập trong mục này một cách hiệu quả, các em cần:
- Nắm vững lý thuyết: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các định nghĩa, tính chất, công thức liên quan đến chủ đề đang xét.
- Hiểu rõ yêu cầu đề bài: Xác định chính xác những gì đề bài hỏi, các dữ kiện đã cho và những gì cần tìm.
- Lựa chọn phương pháp giải phù hợp: Dựa trên kiến thức đã học và đặc điểm của bài toán, chọn phương pháp giải tối ưu nhất.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác và hợp lý.
Nội dung chi tiết Giải mục 2 trang 37, 38
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục này, Tusach.vn sẽ trình bày chi tiết lời giải cho từng bài tập. Chúng ta sẽ cùng nhau phân tích đề bài, xác định phương pháp giải và thực hiện các bước giải một cách cụ thể.
Bài 1: (Ví dụ minh họa - Thay bằng nội dung bài tập thực tế)
Đề bài: (Nêu rõ đề bài)
Lời giải:
Bước 1: ...
Bước 2: ...
Bước 3: ...
Kết luận: ...
Bài 2: (Ví dụ minh họa - Thay bằng nội dung bài tập thực tế)
Đề bài: (Nêu rõ đề bài)
Lời giải:
Bước 1: ...
Bước 2: ...
Bước 3: ...
Kết luận: ...
Các dạng bài tập thường gặp trong mục 2 trang 37, 38
- Dạng 1: Bài tập áp dụng trực tiếp công thức, định lý.
- Dạng 2: Bài tập kết hợp nhiều kiến thức khác nhau.
- Dạng 3: Bài tập nâng cao, đòi hỏi tư duy sáng tạo.
Mẹo giải nhanh và hiệu quả
Để giải các bài tập Toán 11 một cách nhanh chóng và hiệu quả, các em có thể tham khảo một số mẹo sau:
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp các em thực hiện các phép tính phức tạp một cách dễ dàng.
- Vẽ hình minh họa: Vẽ hình minh họa có thể giúp các em hình dung rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
- Luyện tập thường xuyên: Luyện tập thường xuyên là cách tốt nhất để nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
- Các video bài giảng Toán 11
Tusach.vn hy vọng rằng với lời giải chi tiết và những chia sẻ hữu ích trên đây, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 11. Chúc các em học tốt!