Giải mục 3 trang 58, 59, 60 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 58, 59, 60 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 58, 59, 60 trong Chuyên đề học tập Toán 12 Chân trời sáng tạo. Bài giải này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.
Chúng tôi hiểu rằng việc tự học Toán 12 có thể gặp nhiều khó khăn. Do đó, chúng tôi cung cấp lời giải đầy đủ, kèm theo các bước giải chi tiết và giải thích rõ ràng.
Khảo sát 40 học sinh lớp 12A về số xe máy có ở gia đình mỗi bạn. Kết quả được ghi vào bảng tần số sau: Hỏi trung bình trong mỗi gia đình các bạn lớp 12A có bao nhiêu xe máy?
Hoạt động 3
Trả lời câu hỏi Hoạt động 1 trang 58 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Khảo sát 40 học sinh lớp 12A về số xe máy có ở gia đình mỗi bạn. Kết quả được ghi vào bảng tần số sau:

Hỏi trung bình trong mỗi gia đình các bạn lớp 12A có bao nhiêu xe máy?
Phương pháp giải:
Sử dụng công thức tính số trung bình: \(\overline x = \frac{{{m_1}.{x_1} + {m_2}.{x_2} + ... + {m_k}.{x_k}}}{n}\).
Lời giải chi tiết:
Trung bình trong mỗi gia đình các bạn lớp 12A có:
\(\overline x = \frac{{4.0 + 12.1 + 18.2 + 6.3}}{{40}} = 1,65\) (xe máy).
Luyện tập 4
Trả lời câu hỏi Luyện tập 4 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 3 tấm thẻ cùng loại được đánh số từ 1 đến 3.
a) Lấy ra ngẫu nhiên 1 thẻ từ hộp. Gọi X là số ghi trên thẻ đó. Hãy tính kì vọng của X.
b) Lấy ra ngẫu nhiên đồng thời 2 thẻ từ hộp. Gọi Y là số lớn hơn trong hai số ghi trên hai thẻ đó. Hãy tính kì vọng của Y.
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
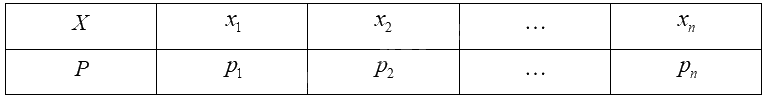
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Lời giải chi tiết:
a) \(X\) nhận các giá trị là 1; 2; 3.
Xác suất để nhận được 3 tấm thẻ là như nhau và bằng: \(\frac{1}{3}\).
Bảng phân bố xác suất của \(X\):
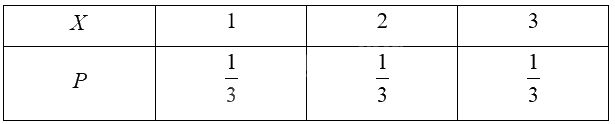
Kì vọng của \(X\) là: \(E\left( X \right) = 1.\frac{1}{3} + 2.\frac{1}{3} + 3.\frac{1}{3} = 2\).
b) \(Y\) nhận các giá trị là 2; 3.
TH1: Lấy ra thẻ 1 và 2. Khi đó: \(Y = 2\).
TH2: Lấy ra thẻ 1 và 3. Khi đó: \(Y = 3\).
TH3: Lấy ra thẻ 2 và 3. Khi đó: \(Y = 3\).
Vậy \(P\left( {Y = 2} \right) = \frac{1}{3},P\left( {Y = 3} \right) = \frac{2}{3}\).
Bảng phân bố xác suất của \(Y\):
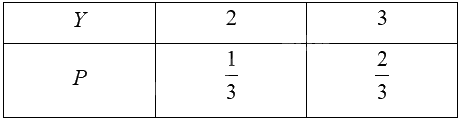
Kì vọng của \(Y\) là: \(E\left( Y \right) = 2.\frac{1}{3} + 3.\frac{2}{3} = \frac{8}{3}\).
Vận dụng 1
Trả lời câu hỏi Vận dụng 1 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Ở một hội chợ, người ta tổ chức trò chơi có thưởng như sau: Có 3 quả bóng giống nhau được đánh số từ 1 đến 3 và 3 cái hộp giống nhau cũng được đánh số từ 1 đến 3. Người chơi bị bịt mắt và phải cho bóng vào hộp sao cho mỗi hộp có đúng 1 quả bóng. Ứng với mỗi quả bóng cho vào hộp có cùng số với nó, người chơi sẽ được thưởng 2000 đồng. Trước mỗi lượt chơi, người chơi phải mua vé ở chỗ quản trò với giá 1.000 đồng. Nếu so sánh về mặt trung bình thì người chơi hay quản trò có lợi hơn?
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
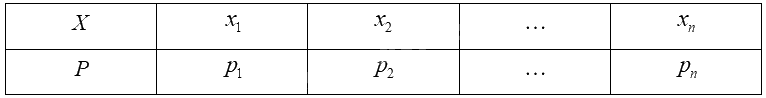
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Lời giải chi tiết:
Gọi \(X\) là số bóng được đặt vào hộp có cùng số với nó, \(Y\) là số tiền người chơi thu được.
Ta có:
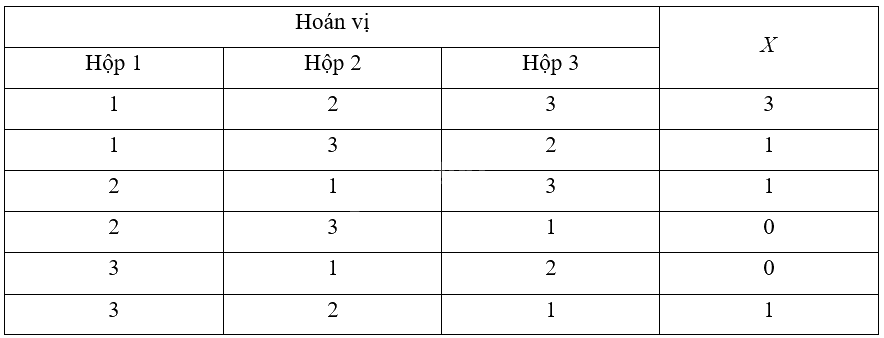
\(X\) nhận các giá trị là 0; 1; 3.
\(Y\) nhận các giá trị là 0; 2000; 6000.
Xác suất để \(Y\) nhận giá trị bằng 0 là: \(\frac{2}{6} = \frac{1}{3}\).
Xác suất để \(Y\) nhận giá trị bằng 2000 là: \(\frac{3}{6} = \frac{1}{2}\).
Xác suất để \(Y\) nhận giá trị bằng 6000 là: \(\frac{1}{6}\).
Bảng phân bố xác suất của \(Y\):
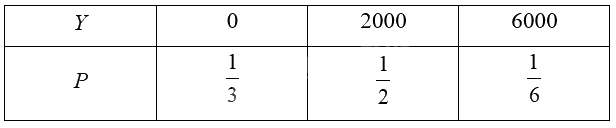
Kì vọng của \(Y\) là: \(E\left( Y \right) = 0.\frac{1}{3} + 2000.\frac{1}{2} + 6000.\frac{1}{6} = 2000\).
Vậy số tiền thưởng trung bình trong mỗi lần chơi là 2000 đồng. Chi phí một lần chơi là 1000 đồng. Vậy xét theo trung bình thì người chơi có lợi hơn.
- Hoạt động 3
- Luyện tập 4
- Vận dụng 1
Trả lời câu hỏi Hoạt động 1 trang 58 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Khảo sát 40 học sinh lớp 12A về số xe máy có ở gia đình mỗi bạn. Kết quả được ghi vào bảng tần số sau:

Hỏi trung bình trong mỗi gia đình các bạn lớp 12A có bao nhiêu xe máy?
Phương pháp giải:
Sử dụng công thức tính số trung bình: \(\overline x = \frac{{{m_1}.{x_1} + {m_2}.{x_2} + ... + {m_k}.{x_k}}}{n}\).
Lời giải chi tiết:
Trung bình trong mỗi gia đình các bạn lớp 12A có:
\(\overline x = \frac{{4.0 + 12.1 + 18.2 + 6.3}}{{40}} = 1,65\) (xe máy).
Trả lời câu hỏi Luyện tập 4 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 3 tấm thẻ cùng loại được đánh số từ 1 đến 3.
a) Lấy ra ngẫu nhiên 1 thẻ từ hộp. Gọi X là số ghi trên thẻ đó. Hãy tính kì vọng của X.
b) Lấy ra ngẫu nhiên đồng thời 2 thẻ từ hộp. Gọi Y là số lớn hơn trong hai số ghi trên hai thẻ đó. Hãy tính kì vọng của Y.
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
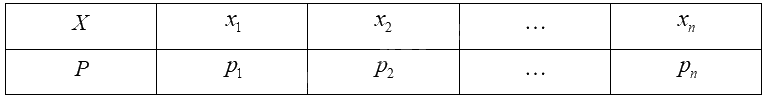
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Lời giải chi tiết:
a) \(X\) nhận các giá trị là 1; 2; 3.
Xác suất để nhận được 3 tấm thẻ là như nhau và bằng: \(\frac{1}{3}\).
Bảng phân bố xác suất của \(X\):
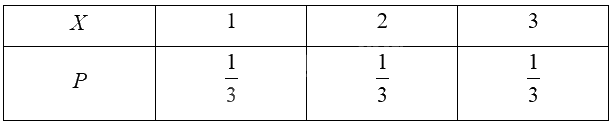
Kì vọng của \(X\) là: \(E\left( X \right) = 1.\frac{1}{3} + 2.\frac{1}{3} + 3.\frac{1}{3} = 2\).
b) \(Y\) nhận các giá trị là 2; 3.
TH1: Lấy ra thẻ 1 và 2. Khi đó: \(Y = 2\).
TH2: Lấy ra thẻ 1 và 3. Khi đó: \(Y = 3\).
TH3: Lấy ra thẻ 2 và 3. Khi đó: \(Y = 3\).
Vậy \(P\left( {Y = 2} \right) = \frac{1}{3},P\left( {Y = 3} \right) = \frac{2}{3}\).
Bảng phân bố xác suất của \(Y\):
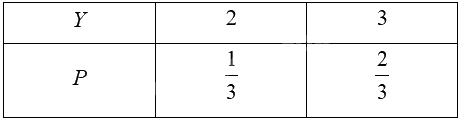
Kì vọng của \(Y\) là: \(E\left( Y \right) = 2.\frac{1}{3} + 3.\frac{2}{3} = \frac{8}{3}\).
Trả lời câu hỏi Vận dụng 1 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Ở một hội chợ, người ta tổ chức trò chơi có thưởng như sau: Có 3 quả bóng giống nhau được đánh số từ 1 đến 3 và 3 cái hộp giống nhau cũng được đánh số từ 1 đến 3. Người chơi bị bịt mắt và phải cho bóng vào hộp sao cho mỗi hộp có đúng 1 quả bóng. Ứng với mỗi quả bóng cho vào hộp có cùng số với nó, người chơi sẽ được thưởng 2000 đồng. Trước mỗi lượt chơi, người chơi phải mua vé ở chỗ quản trò với giá 1.000 đồng. Nếu so sánh về mặt trung bình thì người chơi hay quản trò có lợi hơn?
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
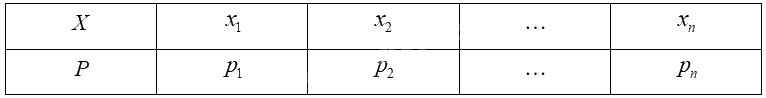
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Lời giải chi tiết:
Gọi \(X\) là số bóng được đặt vào hộp có cùng số với nó, \(Y\) là số tiền người chơi thu được.
Ta có:
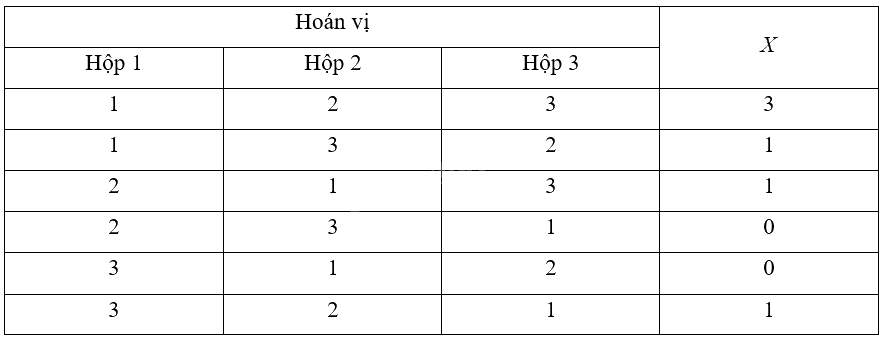
\(X\) nhận các giá trị là 0; 1; 3.
\(Y\) nhận các giá trị là 0; 2000; 6000.
Xác suất để \(Y\) nhận giá trị bằng 0 là: \(\frac{2}{6} = \frac{1}{3}\).
Xác suất để \(Y\) nhận giá trị bằng 2000 là: \(\frac{3}{6} = \frac{1}{2}\).
Xác suất để \(Y\) nhận giá trị bằng 6000 là: \(\frac{1}{6}\).
Bảng phân bố xác suất của \(Y\):
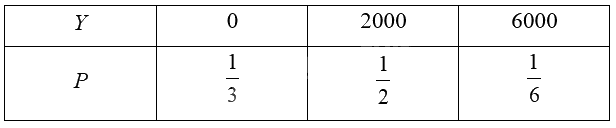
Kì vọng của \(Y\) là: \(E\left( Y \right) = 0.\frac{1}{3} + 2000.\frac{1}{2} + 6000.\frac{1}{6} = 2000\).
Vậy số tiền thưởng trung bình trong mỗi lần chơi là 2000 đồng. Chi phí một lần chơi là 1000 đồng. Vậy xét theo trung bình thì người chơi có lợi hơn.
Giải mục 3 trang 58, 59, 60 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 3 trang 58, 59, 60 trong Chuyên đề học tập Toán 12 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề. Tusach.vn sẽ cung cấp cho bạn lời giải chi tiết, từng bước một, giúp bạn hiểu rõ bản chất của bài toán và cách tiếp cận hiệu quả.
Nội dung chính của Mục 3
Trước khi đi vào giải chi tiết, chúng ta cần xác định nội dung chính của Mục 3. Thông thường, mục này sẽ xoay quanh các khái niệm và định lý quan trọng, cùng với các bài tập vận dụng để kiểm tra mức độ hiểu bài của học sinh. Việc nắm vững lý thuyết là bước đầu tiên quan trọng để giải quyết các bài tập một cách chính xác.
Giải chi tiết từng bài tập trang 58
- Bài tập 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích từng bước).
- Bài tập 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích từng bước).
- Bài tập 3: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích từng bước).
Giải chi tiết từng bài tập trang 59
- Bài tập 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích từng bước).
- Bài tập 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích từng bước).
Giải chi tiết từng bài tập trang 60
- Bài tập 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích từng bước).
- Bài tập 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích từng bước).
Mẹo giải Toán 12 Chân trời sáng tạo hiệu quả
- Nắm vững lý thuyết: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các khái niệm, định lý và công thức quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo các sách bài tập, đề thi thử và các nguồn tài liệu trực tuyến để mở rộng kiến thức.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo để được hướng dẫn và giải đáp.
Tại sao nên chọn Tusach.vn để học Toán 12?
Tusach.vn là một website học tập uy tín, cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 Chân trời sáng tạo. Chúng tôi có đội ngũ giáo viên giàu kinh nghiệm, luôn cập nhật kiến thức mới nhất và sẵn sàng hỗ trợ bạn trong quá trình học tập. Ngoài ra, Tusach.vn còn cung cấp nhiều tài liệu học tập hữu ích khác, giúp bạn đạt kết quả tốt nhất trong kỳ thi THPT Quốc gia.
Hy vọng với lời giải chi tiết và những lời khuyên hữu ích trên, bạn sẽ tự tin hơn trong việc học Toán 12 Chân trời sáng tạo. Chúc bạn học tốt!