Giải bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Một cơ sở đóng thuyền thủ công cần 10 giờ lao động để đóng một thuyền loại A và 15 giờ lao động để đóng một thuyền loại B. Mỗi tuần cơ sở bố trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền này. Qua thực tế, người ta thấy mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B. Mỗi thuyền loại A, loại B cho lợi nhuận lần lượt là 0,5 triệu đồng và 0,7 triệu đồng. Mỗi tuần cơ sở nên đóng bao nhiêu thuyền mỗi loại để có thể thu được lợi nhuận cao nhất?
Đề bài
Một cơ sở đóng thuyền thủ công cần 10 giờ lao động để đóng một thuyền loại A và 15 giờ lao động để đóng một thuyền loại B. Mỗi tuần cơ sở bố trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền này. Qua thực tế, người ta thấy mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B. Mỗi thuyền loại A, loại B cho lợi nhuận lần lượt là 0,5 triệu đồng và 0,7 triệu đồng. Mỗi tuần cơ sở nên đóng bao nhiêu thuyền mỗi loại để có thể thu được lợi nhuận cao nhất?
Phương pháp giải - Xem chi tiết
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết
Gọi \(x,y\left( {x,y \in \mathbb{N}} \right)\) lần lượt là số thuyền loại A, loại B cơ sở đóng được trong một tuần.
Cơ sở chỉ bố trí được tối đa 120 giờ lao động nên ta có \(10x + 15y \le 120\) hay \(2x + 3y - 24 \le 0\).
Mỗi tuần cơ sở bán được tối đa 6 thuyền loại A nên ta có \(x \le 6\).
Mỗi tuần cơ sở bán được tối thiểu 2 thuyền loại B nên ta có \(y \ge 2\).
Lợi nhuận thu được là \(F = 0,5x + 0,7y\) (triệu đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 0,5x + 0,7y \to \max \) với ràng buộc \(\left\{ \begin{array}{l}2x + 3y - 24 \le 0\\x \ge 0\\x \le 6\\y \ge 2\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tứ giác \(ABCD\).
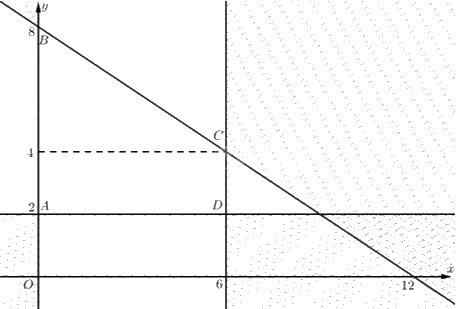
Ta có \(A\left( {0;2} \right),B\left( {0;8} \right),D\left( {6;0} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 24\\x = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = 4\end{array} \right.\). Vậy \(C\left( {6;4} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;2} \right) = 1,4;F\left( {0;8} \right) = 5,6;F\left( {6;4} \right) = 5,8;F\left( {6;2} \right) = 4,4\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {6;4} \right) = 5,8\).
Vậy mỗi tuần cơ sở nên đóng 6 thuyền loại A và 4 thuyền loại B để có thể thu được lợi nhuận cao nhất.
Giải bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp giải
Bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, hoặc các bài toán liên quan đến cực trị của hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, quy tắc tính đạo hàm, và các phương pháp tìm cực trị.
Các kiến thức cần nắm vững trước khi giải bài 3 trang 14
- Đạo hàm: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm.
- Quy tắc tính đạo hàm: Quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Ứng dụng đạo hàm: Khảo sát hàm số, tìm cực trị, tìm khoảng đơn điệu.
- Các dạng bài tập thường gặp: Bài tập về tìm đạo hàm, tìm cực trị, giải phương trình, bất phương trình chứa đạo hàm.
Lời giải chi tiết bài 3 trang 14 (Ví dụ minh họa)
(Lưu ý: Nội dung lời giải chi tiết sẽ phụ thuộc vào đề bài cụ thể của bài 3 trang 14. Dưới đây là một ví dụ minh họa.)
Đề bài: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Lời giải:
- Tính đạo hàm cấp nhất: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
- Khảo sát dấu của đạo hàm:
- Với x < 0, y' > 0, hàm số đồng biến.
- Với 0 < x < 2, y' < 0, hàm số nghịch biến.
- Với x > 2, y' > 0, hàm số đồng biến.
- Kết luận: Hàm số đạt cực đại tại x = 0, ycđ = 2 và đạt cực tiểu tại x = 2, yct = -2.
Mẹo giải bài tập hiệu quả
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
- Vận dụng linh hoạt các kiến thức đã học để giải quyết bài toán.
- Kiểm tra lại kết quả sau khi giải xong để đảm bảo tính chính xác.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Các bài tập tương tự
Để củng cố kiến thức và rèn luyện kỹ năng, bạn có thể tham khảo thêm các bài tập tương tự sau:
- Bài 1 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
- Bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
- Các bài tập khác trong chương trình Toán 12.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn là website cung cấp lời giải bài tập Toán 12 nhanh chóng, chính xác và dễ hiểu. Chúng tôi luôn cố gắng mang đến cho học sinh những tài liệu học tập tốt nhất, giúp các bạn học tập hiệu quả và đạt kết quả cao. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 12 | https://tusach.vn/toan-12 |
| Chuyên đề học tập Toán 12 | https://tusach.vn/toan-12/chuyen-de-hoc-tap |