Giải bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 4 trang 14 trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi sẽ phân tích từng bước giải, giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết các bài toán tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Để làm một chiếc bánh bao loại X cần 100 g bột mì và 60 g thịt nạc vai. Để làm một chiếc bánh bao loại Y cần 150 g bột mì và 30 g thịt nạc vai. Có thể làm được nhiều nhất bao nhiêu chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn? Biết rằng không thiếu các nguyên liệu khác để làm bánh.
Đề bài
Để làm một chiếc bánh bao loại X cần 100 g bột mì và 60 g thịt nạc vai. Để làm một chiếc bánh bao loại Y cần 150 g bột mì và 30 g thịt nạc vai. Có thể làm được nhiều nhất bao nhiêu chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn? Biết rằng không thiếu các nguyên liệu khác để làm bánh.
Phương pháp giải - Xem chi tiết
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết
Gọi \(x,y\left( {x,y \in \mathbb{N}} \right)\) lần lượt là số bánh bao loại X, loại Y làm được.
Có sẵn \(3kg = 3000g\) bột mì nên ta có \(100x + 150y \le 3000\) hay \(2x + 3y - 60 \le 0\).
Có sẵn \(1,2kg = 1200g\) thịt nạc vai nên ta có \(60x + 30y \le 1200\) hay \(2x + y - 40 \le 0\).
Số bánh bao làm được là \(F = x + y\) (chiếc).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = x + y \to \max \) với ràng buộc \(\left\{ \begin{array}{l}2x + 3y - 60 \le 0\\2x + y - 40 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tứ giác \(OABC\).
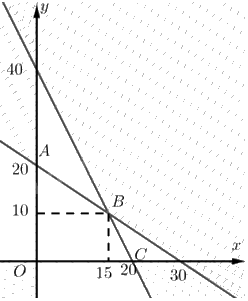
Ta có \(A\left( {0;20} \right),C\left( {20;0} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 60\\2{\rm{x}} + y = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 15\\y = 10\end{array} \right.\). Vậy \(B\left( {15;10} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;20} \right) = 20;F\left( {15;10} \right) = 25;F\left( {6;2} \right) = 8\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {15;10} \right) = 25\).
Vậy làm được nhiều nhất 15 cái bánh bao loại X và 10 cái bánh bao loại Y.
Giải bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Phân tích chi tiết và hướng dẫn giải
Bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, hoặc các bài toán liên quan đến giới hạn. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, quy tắc tính đạo hàm, và các phương pháp giải quyết bài toán liên quan.
I. Tóm tắt lý thuyết cần thiết
Trước khi đi vào giải bài tập cụ thể, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
- Đạo hàm: Đạo hàm của hàm số f(x) tại điểm x, ký hiệu là f'(x), biểu thị tốc độ thay đổi tức thời của hàm số tại điểm đó.
- Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp, và các hàm số cơ bản (hàm số mũ, hàm số logarit, hàm lượng giác).
- Ứng dụng đạo hàm: Sử dụng đạo hàm để tìm cực trị của hàm số, khảo sát sự biến thiên của hàm số, và giải các bài toán tối ưu.
II. Giải bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo (Ví dụ minh họa)
(Giả sử bài 4 yêu cầu khảo sát hàm số y = x3 - 3x2 + 2)
- Xác định tập xác định: Hàm số y = x3 - 3x2 + 2 có tập xác định là D = ℝ.
- Tính đạo hàm cấp nhất: y' = 3x2 - 6x.
- Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
- Khảo sát hàm số:
- Với x < 0, y' > 0, hàm số đồng biến.
- Với 0 < x < 2, y' < 0, hàm số nghịch biến.
- Với x > 2, y' > 0, hàm số đồng biến.
- Tìm cực trị:
- Tại x = 0, hàm số đạt cực đại, giá trị cực đại là y(0) = 2.
- Tại x = 2, hàm số đạt cực tiểu, giá trị cực tiểu là y(2) = -2.
- Tìm giới hạn vô cùng:
- limx→+∞ y = +∞
- limx→-∞ y = -∞
- Vẽ đồ thị hàm số: Dựa vào các kết quả trên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
III. Mẹo giải bài tập và lưu ý quan trọng
Để giải quyết các bài toán tương tự một cách nhanh chóng và chính xác, bạn nên:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán.
- Sử dụng công thức và quy tắc: Áp dụng các công thức và quy tắc đạo hàm một cách chính xác.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là hợp lý và chính xác.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và nâng cao kiến thức.
IV. Tài liệu tham khảo thêm
Để hiểu sâu hơn về các kiến thức liên quan, bạn có thể tham khảo:
- Sách giáo khoa Toán 12 - Chân trời sáng tạo
- Các tài liệu ôn thi THPT Quốc gia
- Các trang web học Toán trực tuyến uy tín như Tusach.vn
Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn giải quyết bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt!