Giải bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 7 trang 22 trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi sẽ phân tích từng bước, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Giải bài toán quy hoạch tuyến tính: \(F = 3x + 5y \to \min \) với ràng buộc \(\left\{ \begin{array}{l}2{\rm{x}} - y + 4 \ge 0\\4{\rm{x}} + 3y \ge 12\\2{\rm{x}} - 3y \le 6\end{array} \right.\)
Đề bài
Giải bài toán quy hoạch tuyến tính:
\(F = 3x + 5y \to \min \)
với ràng buộc
\(\left\{ \begin{array}{l}2{\rm{x}} - y + 4 \ge 0\\4{\rm{x}} + 3y \ge 12\\2{\rm{x}} - 3y \le 6\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết
Viết lại ràng buộc
\(\left\{ \begin{array}{l}2{\rm{x}} - y \ge - 4\\4{\rm{x}} + 3y \ge 12\\2{\rm{x}} - 3y \le 6\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
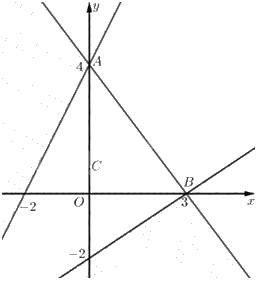
Ta có \(A\left( {0;4} \right),B\left( {3;0} \right)\).
Do \({\Omega }\) nằm trong góc phần tư thứ nhất và các hệ số của biểu thức \(F = 3x + 5y\) đều dương nên \(F\) đạt giá trị nhỏ nhất tại một đỉnh của \({\Omega }\).
Ta có \(F\left( {0;4} \right) = 40,F\left( {3;0} \right) = 9\).
Do đó \(\mathop {\min }\limits_{\Omega } F = F\left( {3;0} \right) = 9\).
Giải bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình. Để giải quyết bài toán này hiệu quả, học sinh cần nắm vững kiến thức nền tảng và áp dụng các phương pháp giải phù hợp. Bài viết này sẽ đi sâu vào phân tích chi tiết từng phần của bài toán, cung cấp lời giải chi tiết và các lưu ý quan trọng.
Nội dung bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Thông thường, bài 7 trang 22 sẽ bao gồm các dạng bài tập sau:
- Dạng 1: Bài tập về lý thuyết, yêu cầu học sinh trình bày định nghĩa, tính chất hoặc định lý liên quan.
- Dạng 2: Bài tập áp dụng công thức, yêu cầu học sinh sử dụng công thức để tính toán và tìm ra kết quả.
- Dạng 3: Bài tập kết hợp lý thuyết và công thức, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết vấn đề.
- Dạng 4: Bài tập nâng cao, đòi hỏi học sinh phải có tư duy logic và khả năng phân tích tốt.
Lời giải chi tiết bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài 7 trang 22, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài toán. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 7, ví dụ:)
Ví dụ: Giải câu a) bài 7 trang 22
Đề bài: (Giả sử đề bài câu a)
Lời giải:
- Bước 1: Phân tích đề bài và xác định yêu cầu.
- Bước 2: Áp dụng công thức hoặc định lý liên quan.
- Bước 3: Thực hiện các phép tính và tìm ra kết quả.
- Bước 4: Kiểm tra lại kết quả và kết luận.
Ví dụ: Giải câu b) bài 7 trang 22
Đề bài: (Giả sử đề bài câu b)
Lời giải:
(Tương tự như giải câu a)
Mẹo giải nhanh bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Để giải bài 7 trang 22 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Sử dụng sơ đồ Venn hoặc bảng biểu để tóm tắt thông tin.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.
- Tham khảo các nguồn tài liệu tham khảo khác để mở rộng kiến thức.
Lưu ý quan trọng khi giải bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Khi giải bài 7 trang 22, bạn cần lưu ý một số điểm sau:
- Kiểm tra kỹ các điều kiện của bài toán.
- Sử dụng đúng đơn vị đo.
- Trình bày lời giải một cách rõ ràng và logic.
- Kiểm tra lại kết quả trước khi nộp bài.
Tusach.vn - Đồng hành cùng bạn học Toán 12
Tusach.vn là website cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12, bao gồm cả Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi hy vọng rằng bài viết này sẽ giúp bạn hiểu rõ hơn về bài 7 trang 22 và đạt kết quả tốt trong học tập. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chủ đề | Liên kết |
|---|---|
| Giải Toán 12 Chân trời sáng tạo | https://tusach.vn/toan-12-chan-troi-sang-tao |
| Chuyên đề học tập Toán 12 | https://tusach.vn/chuyen-de-hoc-tap-toan-12 |