Giải bài 1 trang 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 1 trang 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 1 trang 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 12 mới nhất.
Giải bài toán quy hoạch tuyến tính: (F = 8x + 5y to max ,min ) với ràng buộc (left{ begin{array}{l}2{rm{x}} + y le 8\x ge 0\x le 3\y ge 1\y le 5end{array} right.)
Đề bài
Giải bài toán quy hoạch tuyến tính:
\(F = 8x + 5y \to \max ,\min \)
với ràng buộc
\(\left\{ \begin{array}{l}2{\rm{x}} + y \le 8\\x \ge 0\\x \le 3\\y \ge 1\\y \le 5\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết
Tập phương án \({\Omega }\) là miền ngũ giác \(ABCDE\).
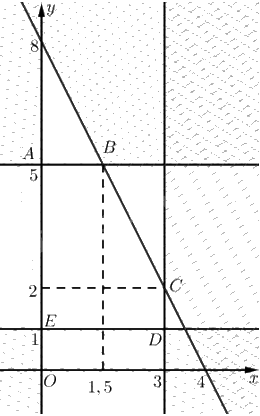
Ta có: \(A\left( {0;5} \right),D\left( {3;1} \right),E\left( {0;1} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x + y = 8\\y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1,5\\y = 5\end{array} \right.\). Vậy \(B\left( {1,5;5} \right)\)
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x + y = 8\\x = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right.\). Vậy \(C\left( {3;2} \right)\)
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;5} \right) = 25,F\left( {1,5;5} \right) = 37,F\left( {3;2} \right) = 34,F\left( {3;0} \right) = 24,F\left( {0;1} \right) = 5\).
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {1,5;5} \right) = 37;\mathop {\min }\limits_{\Omega } F = F\left( {0;1} \right) = 5\).
Giải bài 1 trang 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 1 trang 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào việc ôn tập và củng cố kiến thức về một chủ đề cụ thể trong chương trình. Nội dung bài tập có thể liên quan đến giới hạn, đạo hàm, tích phân, hoặc các chủ đề khác tùy thuộc vào chương học. Việc nắm vững kiến thức nền tảng và áp dụng đúng các công thức, định lý là chìa khóa để giải quyết bài tập một cách hiệu quả.
Nội dung chi tiết bài 1 trang 13
Để giải quyết bài 1 trang 13, chúng ta cần phân tích kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho. Sau đó, áp dụng các kiến thức và kỹ năng đã học để tìm ra lời giải chính xác. Dưới đây là lời giải chi tiết cho từng phần của bài tập:
Phần 1: (Ví dụ, giả sử bài tập yêu cầu tính giới hạn)
Để tính giới hạn của một hàm số, chúng ta có thể sử dụng các phương pháp như phân tích thành nhân tử, chia cả tử và mẫu cho một biểu thức chứa n, hoặc sử dụng quy tắc L'Hopital. Ví dụ:
lim (x->2) (x^2 - 4) / (x - 2) = lim (x->2) (x - 2)(x + 2) / (x - 2) = lim (x->2) (x + 2) = 4
Phần 2: (Ví dụ, giả sử bài tập yêu cầu tính đạo hàm)
Để tính đạo hàm của một hàm số, chúng ta cần áp dụng các quy tắc đạo hàm cơ bản như quy tắc lũy thừa, quy tắc tích, quy tắc thương, và quy tắc chuỗi. Ví dụ:
y = x^3 + 2x^2 - 5x + 1
y' = 3x^2 + 4x - 5
Phần 3: (Ví dụ, giả sử bài tập yêu cầu tính tích phân)
Để tính tích phân của một hàm số, chúng ta cần tìm nguyên hàm của hàm số đó. Sau đó, áp dụng định lý cơ bản của tích phân để tính giá trị của tích phân xác định. Ví dụ:
∫x^2 dx = (x^3)/3 + C
Mẹo giải bài tập Toán 12 hiệu quả
- Nắm vững kiến thức nền tảng: Hiểu rõ các định nghĩa, định lý, và công thức là bước đầu tiên để giải quyết bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn làm quen với các dạng bài và rèn luyện kỹ năng giải quyết vấn đề.
- Sử dụng tài liệu tham khảo: Sách giáo khoa, sách bài tập, và các trang web học tập trực tuyến là những nguồn tài liệu hữu ích.
- Hỏi thầy cô hoặc bạn bè: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô hoặc bạn bè để được giúp đỡ.
Tusach.vn - Đồng hành cùng bạn học Toán 12
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập Toán 12. Chúng tôi luôn cập nhật nội dung mới nhất và đa dạng các dạng bài tập để đáp ứng nhu cầu học tập của học sinh. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 12 Chân trời sáng tạo | https://tusach.vn/toan-12-chan-troi-sang-tao |
| Chuyên đề học tập Toán 12 | https://tusach.vn/chuyen-de-toan-12 |