Giải bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 14 trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi sẽ phân tích từng bước giải, giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết các bài toán tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Hãy cùng khám phá lời giải chi tiết ngay sau đây!
Giải bài toán quy hoạch tuyến tính: (F = 10x + 20y to min ) với ràng buộc (left{ begin{array}{l}20{rm{x}} + 5y ge 40\16{rm{x}} + 60y ge 120\x - y le 3\x ge 0\y ge 0end{array} right.)
Đề bài
Giải bài toán quy hoạch tuyến tính:
\(F = 10x + 20y \to \min \)
với ràng buộc
\(\left\{ \begin{array}{l}20{\rm{x}} + 5y \ge 40\\16{\rm{x}} + 60y \ge 120\\x - y \le 3\\x \ge 0\\y \ge 0\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
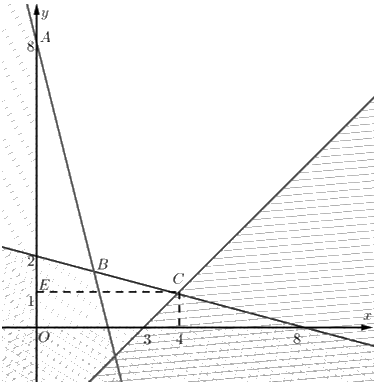
Ta có \(A\left( {0;8} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}20{\rm{x}} + 5y = 40\\15{\rm{x}} + 60y = 120\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{8}{5}\\y = \frac{8}{5}\end{array} \right.\). Vậy \(B\left( {\frac{8}{5};\frac{8}{5}} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x - y = 3\\15{\rm{x}} + 60y = 120\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right.\). Vậy \(C\left( {4;1} \right)\).
Do \({\Omega }\) nằm trong góc phần tư thứ nhất và các hệ số của biểu thức \(F = 10x + 20y\) đều dương nên \(F\) đạt giá trị nhỏ nhất tại một đỉnh của \({\Omega }\).
Ta có \(F\left( {0;8} \right) = 160;F\left( {\frac{8}{5};\frac{8}{5}} \right) = 48;F\left( {4;1} \right) = 60\).
Do đó \(F\) đạt giá trị nhỏ nhất tại đỉnh \(B\left( {\frac{8}{5};\frac{8}{5}} \right)\) và \(\mathop {\min }\limits_{\Omega } F = B\left( {\frac{8}{5};\frac{8}{5}} \right) = 48\).
Giải bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Phân tích chi tiết và hướng dẫn giải
Bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm, tích phân, hoặc các ứng dụng của đạo hàm và tích phân trong thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức và kỹ năng giải toán liên quan.
I. Đề bài và yêu cầu
Trước khi đi vào giải chi tiết, chúng ta cần xác định rõ đề bài và yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu tính đạo hàm, tìm cực trị, hoặc giải phương trình, bất phương trình liên quan đến hàm số.
II. Phương pháp giải
Để giải bài 2 trang 14, chúng ta có thể áp dụng các phương pháp sau:
- Phương pháp đạo hàm: Sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số.
- Phương pháp tích phân: Sử dụng tích phân để tính diện tích, thể tích, hoặc giải phương trình tích phân.
- Phương pháp biến đổi tương đương: Sử dụng các phép biến đổi tương đương để đơn giản hóa bài toán.
- Phương pháp xét hàm số: Phân tích tính chất của hàm số để đưa ra kết luận.
III. Lời giải chi tiết
Dưới đây là lời giải chi tiết cho bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo (giả sử đề bài cụ thể là tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1):
- Bước 1: Xác định quy tắc đạo hàm cần sử dụng. Trong trường hợp này, chúng ta sử dụng quy tắc đạo hàm của tổng, hiệu và lũy thừa.
- Bước 2: Áp dụng quy tắc đạo hàm để tính đạo hàm của từng thành phần trong hàm số.
- Bước 3: Tổng hợp kết quả để có được đạo hàm của hàm số f(x).
Vậy, f'(x) = 3x2 - 6x + 2.
IV. Lưu ý khi giải bài tập
Khi giải bài tập Toán 12, đặc biệt là các bài tập trong Chuyên đề học tập, bạn cần lưu ý những điều sau:
- Đọc kỹ đề bài: Đảm bảo bạn hiểu rõ yêu cầu của bài toán.
- Nắm vững kiến thức: Ôn tập lại các khái niệm, công thức và kỹ năng liên quan.
- Lập kế hoạch giải: Xác định các bước cần thực hiện để giải quyết bài toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác.
V. Bài tập tương tự
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự sau:
- Bài 1 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
- Bài 3 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
VI. Kết luận
Hy vọng với lời giải chi tiết và hướng dẫn giải trên, bạn đã hiểu rõ cách giải bài 2 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong kỳ thi!
| Công thức | Mô tả |
|---|---|
| f'(x) | Đạo hàm của hàm số f(x) |
| ∫f(x)dx | Tích phân của hàm số f(x) |
| Nguồn: tusach.vn | |