Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 63 trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.

Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.

Sau khi khảo sát hiệu quả sử dụng của các cột sạc ô tô điện ở một khu vực, người ta thu được bảng phân bố xác suất của số lượng xe, kí hiệu là X, sạc điện ở mỗi cột sạc trong một ngày như sau: a) Tìm (p). b) Hỏi trung bình một ngày có bao nhiêu xe được sạc điện ở một cột sạc? c) Tính độ lệch chuẩn của (X).

Đề bài

Sau khi khảo sát hiệu quả sử dụng của các cột sạc ô tô điện ở một khu vực, người ta thu được bảng phân bố xác suất của số lượng xe, kí hiệu là X, sạc điện ở mỗi cột sạc trong một ngày như sau:

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 1 a) Tìm \(p\). b) Hỏi trung bình một ngày có bao nhiêu xe được sạc điện ở một cột sạc? c) Tính độ lệch chuẩn của \(X\).

Phương pháp giải - Xem chi tiết Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 2

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

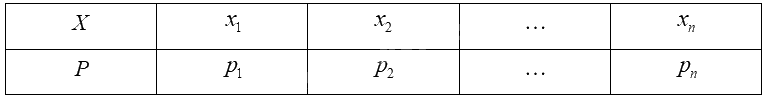
Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 3

Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).

Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).

Độ lệch chuẩn của \(X\) được tính bởi công thức: \(\sigma \left( X \right) = \sqrt {V\left( X \right)} \).

Lời giải chi tiết

a) Ta có: \(0,1 + p + 4p + 3p + p = 1 \Leftrightarrow 0,1 + 9p = 1 \Leftrightarrow p = 0,1\).

b) Bảng phân bố xác suất của \(X\):

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 4

Kì vọng của \(X\) là: \(E\left( X \right) = 0.0,1 + 1.0,1 + 2.0,4 + 3.0,3 + 4.0,1 = 2,2\).

Trung bình một ngày có 2,2 xe được sạc điện ở một cột sạc.

c) Phương sai của \(X\) là: \(V\left( X \right) = {0^2}.0,1 + {1^2}.0,1 + {2^2}.0,4 + {3^2}.0,3 + {4^2}.0,1 - {2,2^2} = 1,16\).

Phương sai của \(X\) là: \(\sigma \left( X \right) = \sqrt {1,16} \approx 1,08\).

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp

Bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức đã học. Ngoài ra, việc luyện tập thường xuyên với các bài tập tương tự cũng rất quan trọng để củng cố kiến thức và rèn luyện kỹ năng giải bài tập.

Nội dung chi tiết bài 2 trang 63

Để cung cấp một giải pháp toàn diện, chúng ta cần xem xét nội dung cụ thể của bài 2. Thông thường, bài tập này có thể thuộc một trong các dạng sau:

Dạng 1: Bài tập về hàm số và đồ thị: Yêu cầu tìm tập xác định, tập giá trị, điểm cực trị, điểm uốn, hoặc vẽ đồ thị hàm số.
Dạng 2: Bài tập về đạo hàm: Yêu cầu tính đạo hàm, tìm cực trị, hoặc giải phương trình, bất phương trình chứa đạo hàm.
Dạng 3: Bài tập về tích phân: Yêu cầu tính tích phân, ứng dụng tích phân để tính diện tích, thể tích.
Dạng 4: Bài tập về số phức: Yêu cầu thực hiện các phép toán với số phức, tìm nghiệm của phương trình bậc hai với hệ số phức.

Lời giải chi tiết bài 2 trang 63 (Ví dụ minh họa)

Giả sử bài 2 trang 63 yêu cầu tính đạo hàm của hàm số f(x) = x³ - 3x² + 2x - 1.

Lời giải:

f'(x) = 3x² - 6x + 2

Vậy, đạo hàm của hàm số f(x) là f'(x) = 3x² - 6x + 2.

Mẹo giải bài tập Toán 12 hiệu quả

Nắm vững kiến thức lý thuyết: Đây là nền tảng quan trọng nhất để giải quyết mọi bài tập.
Đọc kỹ đề bài: Hiểu rõ yêu cầu của đề bài trước khi bắt đầu giải.
Sử dụng công thức và định lý một cách chính xác: Tránh nhầm lẫn trong việc áp dụng công thức.
Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để củng cố kiến thức và kỹ năng.

Tusach.vn – Người bạn đồng hành đáng tin cậy

Tusach.vn cung cấp đầy đủ đáp án, lời giải chi tiết và các bài tập tương tự để giúp bạn học Toán 12 một cách hiệu quả nhất. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các phương pháp giải bài tập sáng tạo, giúp bạn tự tin chinh phục môn Toán.

Bảng tổng hợp các dạng bài tập thường gặp

Dạng bài tập	Phương pháp giải	Ví dụ
Tính đạo hàm	Sử dụng các quy tắc tính đạo hàm	f(x) = x² + 2x + 1
Tìm cực trị	Giải phương trình f'(x) = 0	f(x) = x³ - 3x² + 2x
Tính tích phân	Sử dụng các phương pháp tính tích phân cơ bản	∫(x² + 1) dx

Hy vọng với những hướng dẫn chi tiết này, bạn sẽ giải quyết thành công bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúc bạn học tập tốt!

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp

Nội dung chi tiết bài 2 trang 63

Lời giải chi tiết bài 2 trang 63 (Ví dụ minh họa)

Mẹo giải bài tập Toán 12 hiệu quả

Tusach.vn – Người bạn đồng hành đáng tin cậy

Bảng tổng hợp các dạng bài tập thường gặp

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN