Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án, phương pháp giải và các lưu ý quan trọng để giúp các em nắm vững kiến thức và tự tin làm bài tập.

Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.

Chi phí để sản xuất (x) sản phẩm là (Cleft( x right) = 2500 + 10x + frac{1}{4}{x^2}) (nghìn đồng). Chi phí trung bình trên mỗi sản phẩm là thấp nhất khi số lượng sản phẩm được sản xuất là A. 20. B. 50. C. 100. D. 1000.

Đề bài

Chi phí để sản xuất \(x\) sản phẩm là \(C\left( x \right) = 2500 + 10x + \frac{1}{4}{x^2}\) (nghìn đồng). Chi phí trung bình trên mỗi sản phẩm là thấp nhất khi số lượng sản phẩm được sản xuất là

A. 20.

B. 50.

C. 100.

D. 1000.

Phương pháp giải - Xem chi tiết Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 1

• Chi phí trung bình để sản xuất một sản phẩm là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\).

• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:

‒ Lập bảng biến thiên của hàm số trên tập hợp đó.

‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.

Lời giải chi tiết

Chi phí trung bình để sản xuất mỗi sản phẩm là

\(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2500 + 10x + \frac{1}{4}{x^2}}}{x} = \frac{{2500}}{x} + 10 + \frac{x}{4}\) với \(x > 0\).

b) Ta có: \(\overline C '\left( x \right) = - \frac{{10}}{{{x^2}}} + 0,001\)

\(\overline C '\left( x \right) = 0 \Leftrightarrow - \frac{{10}}{{{x^2}}} + 0,001 = 0 \Leftrightarrow {x^2} = 10000 \Leftrightarrow x = 100\) hoặc \(x = - 100\) (loại).

Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):

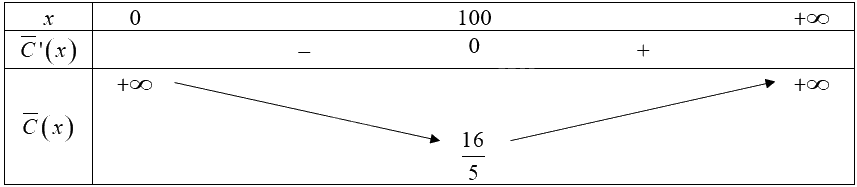
Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 2

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S = f\left( {100} \right) = \frac{{16}}{5}\).

Vậy chi phí trung bình để sản xuất một sản phẩm thấp nhất khi mỗi tuần xưởng sản xuất 100 nghìn sản phẩm.

Chọn C

Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp

Bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững kiến thức nền tảng, hiểu rõ yêu cầu của đề bài và áp dụng các phương pháp giải phù hợp.

Nội dung chính của bài 5 trang 22

Thông thường, bài 5 trang 22 sẽ xoay quanh các chủ đề như:

Đạo hàm và ứng dụng của đạo hàm: Tính đạo hàm, tìm cực trị, khảo sát hàm số.
Tích phân và ứng dụng của tích phân: Tính tích phân, tính diện tích hình phẳng.
Số phức: Các phép toán trên số phức, phương trình bậc hai với hệ số phức.
Hình học không gian: Quan hệ vuông góc trong không gian, khoảng cách giữa hai đường thẳng, giữa đường thẳng và mặt phẳng.

Phương pháp giải bài tập hiệu quả

Đọc kỹ đề bài: Xác định rõ yêu cầu của đề bài, các dữ kiện đã cho và kết quả cần tìm.
Xây dựng phương án giải: Lựa chọn phương pháp giải phù hợp với từng dạng bài tập.
Thực hiện các phép tính: Thực hiện các phép tính một cách chính xác và cẩn thận.
Kiểm tra lại kết quả: Kiểm tra lại kết quả để đảm bảo tính đúng đắn.

Lời giải chi tiết bài 5 trang 22 (Ví dụ)

Để minh họa, chúng ta sẽ cùng giải một bài tập mẫu thuộc bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. (Giả sử bài tập là về đạo hàm)

Bài tập: Cho hàm số y = x³ - 3x² + 2. Tìm cực trị của hàm số.

Lời giải:

Tính đạo hàm bậc nhất: y' = 3x² - 6x
Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
Xác định loại cực trị:
- Với x < 0, y' > 0, hàm số đồng biến.
- Với 0 < x < 2, y' < 0, hàm số nghịch biến.
- Với x > 2, y' > 0, hàm số đồng biến.
Vậy hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Các bài tập tương tự và luyện tập

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Tusach.vn cung cấp nhiều bài tập luyện tập đa dạng với lời giải chi tiết, giúp các em tự tin hơn trong quá trình học tập.

Bảng tổng hợp các dạng bài tập thường gặp

Dạng bài tập	Phương pháp giải
Tính đạo hàm	Sử dụng các quy tắc tính đạo hàm.
Tìm cực trị	Giải phương trình đạo hàm bằng 0 và xét dấu đạo hàm.
Tính tích phân	Sử dụng các phương pháp tính tích phân cơ bản.

Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ hiểu rõ hơn về bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo và đạt kết quả tốt trong các kỳ thi sắp tới. Chúc các em học tập tốt!

Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp

Nội dung chính của bài 5 trang 22

Phương pháp giải bài tập hiệu quả

Lời giải chi tiết bài 5 trang 22 (Ví dụ)

Các bài tập tương tự và luyện tập

Bảng tổng hợp các dạng bài tập thường gặp

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN