Giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập hiệu quả, giúp học sinh nắm vững kiến thức và tự tin làm bài.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Một giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi p
Đề bài
Một giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi phí lắp đặt nhất?
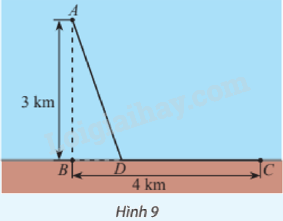
Phương pháp giải - Xem chi tiết
• Đặt \(BD = x\), biểu thị chi phí lắp đặt thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\):
Bước 1. Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 2. Tính \(f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);f\left( b \right)\).
Bước 3. Gọi \(M\) là số lớn nhất và \(m\) là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\).
Lời giải chi tiết
Đặt \(BD = x\left( {km} \right)\left( {0 \le x \le 4} \right)\).
Gọi \(a\) là chi phí lắp đặt cho mỗi kilômét đường ống đặt trên bờ.
Khi đó \(2a\) là chi phí lắp đặt cho mỗi kilômét đường ống đặt dưới biển.
Ta có: \(C{\rm{D}} = BC - B{\rm{D}} = 4 - x,A{\rm{D}} = \sqrt {A{B^2} + B{{\rm{D}}^2}} = \sqrt {{x^2} + 9} \).
Chi phí lắp đặt đường ống là: \(2{\rm{a}}\sqrt {{x^2} + 9} + a\left( {4 - x} \right) = a\left( {2\sqrt {{x^2} + 9} + 4 - x} \right)\).
Xét hàm số \(f\left( x \right) = 2\sqrt {{x^2} + 9} + 4 - x\) trên đoạn \(\left[ {0;4} \right]\).
Ta có: \(f'\left( x \right) = 2.\frac{{{{\left( {{x^2} + 9} \right)}^\prime }}}{{2\sqrt {{x^2} + 9} }} - 1 = \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} - 1\)
\(f'\left( x \right) = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} - 1 = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} = 1 \Leftrightarrow \sqrt {{x^2} + 9} = 2{\rm{x}} \Leftrightarrow {x^2} + 9 = 4{{\rm{x}}^2} \Leftrightarrow {{\rm{x}}^2} = 3 \Leftrightarrow x = \sqrt 3 \) hoặc \(x = - \sqrt 3 \) (loại).
\(f\left( 0 \right) = 10;f\left( {\sqrt 3 } \right) = 4 + 3\sqrt 3 ;f\left( 4 \right) = 10\).
Vậy \(\mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( {\sqrt 3 } \right) = 4 + 3\sqrt 3 \).
Vậy chi phí lắp đặt thấp nhất khi \(x = \sqrt 3 \approx 1,7\left( {km} \right)\).
Giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này, giúp bạn hiểu rõ bản chất và phương pháp giải.
Nội dung bài tập
Trước khi đi vào giải bài, chúng ta cần hiểu rõ yêu cầu của bài tập. Bài 4 trang 21 thường liên quan đến việc tìm đạo hàm của hàm số, xét tính đơn điệu của hàm số, hoặc tìm cực trị của hàm số. Đọc kỹ đề bài và xác định rõ các yếu tố cần tìm là bước đầu tiên quan trọng.
Phương pháp giải
Để giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo, bạn cần nắm vững các kiến thức sau:
- Đạo hàm: Định nghĩa, các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
- Tính đơn điệu của hàm số: Mối liên hệ giữa đạo hàm và tính đơn điệu. Hàm số đồng biến khi đạo hàm dương, nghịch biến khi đạo hàm âm.
- Cực trị của hàm số: Điều kiện để hàm số đạt cực đại, cực tiểu.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x. Ta thực hiện như sau:
- f'(x) = 3x2 - 6x + 2
Các dạng bài tập thường gặp
Bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo có thể xuất hiện dưới nhiều dạng khác nhau. Dưới đây là một số dạng bài tập thường gặp:
- Dạng 1: Tìm đạo hàm của hàm số.
- Dạng 2: Xét tính đơn điệu của hàm số.
- Dạng 3: Tìm cực trị của hàm số.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán thực tế.
Lưu ý khi giải bài tập
Để giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, bạn cần lưu ý những điều sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Nắm vững các kiến thức về đạo hàm, tính đơn điệu, cực trị.
- Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng bài tập.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp tài liệu học tập Toán 12 uy tín và chất lượng. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và chuyên đề học tập. Ngoài ra, chúng tôi còn cung cấp các bài giảng video, bài tập trắc nghiệm và các tài liệu tham khảo khác để giúp bạn học tập Toán 12 hiệu quả hơn.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chuyên đề | Bài tập | Lời giải |
|---|---|---|
| Đạo hàm | Bài 4 trang 21 | Xem tại đây |
| Tính đơn điệu | Bài 5 trang 25 | Xem tại đây |