Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Tusach.vn xin giới thiệu lời giải chi tiết bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tốt nhất cho quá trình học tập của bạn.

Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1800 m3 và chiều sâu 2 m (Hình 7). Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Cần chọn chiều dài và chiều rộng của bể bằng bao nhiêu để tiết kiệm chi phí xây dựng bể nhất?

Đề bài

Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1800 m³ và chiều sâu 2 m (Hình 7). Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Cần chọn chiều dài và chiều rộng của bể bằng bao nhiêu để tiết kiệm chi phí xây dựng bể nhất?

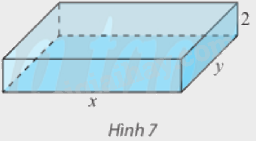
Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 2

• Tìm mối quan hệ giữa \(x,y\), biểu thị chi phí xây dựng bể thông qua các đại lượng đã biết và ẩn.

• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:

‒ Lập bảng biến thiên của hàm số trên tập hợp đó.

‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.

Lời giải chi tiết

Gọi \(a\) là chi phí xây mỗi mét vuông thành bể.

Chi phí xây mỗi mét vuông đáy bể là \(2{\rm{a}}\).

Thể tích của bể là: \(2{\rm{x}}y\left( {{m^3}} \right)\).

Do bể có thể tích 1800 m³ nên ta có: \(2{\rm{x}}y = 1800 \Rightarrow y = \frac{{900}}{x}\).

Diện tích đáy bể là: \(xy = x.\frac{{900}}{x} = 900\left( {{m^2}} \right)\).

Diện tích thành bể là: \(2\left( {x + y} \right).2 = 4{\rm{x}} + 4y = 4{\rm{x}} + 4.\frac{{900}}{x} = 4{\rm{x}} + \frac{{3600}}{x}\left( {{m^2}} \right)\).

Chi phí xây bể là: \(P = 2a.900 + a.\left( {4{\rm{x}} + \frac{{3600}}{x}} \right) = 4a\left( {450 + x + \frac{{900}}{x}} \right)\) với \(x > 0\).

Xét hàm số \(f\left( x \right) = 450 + x + \frac{{900}}{x}\) trên khoảng \(\left( {0; + \infty } \right)\).

Ta có: \(f'\left( x \right) = 1 - \frac{{900}}{{{x^2}}}\)

\(f'\left( x \right) = 0 \Leftrightarrow 1 - \frac{{900}}{{{x^2}}} = 0 \Leftrightarrow {x^2} = 900 \Leftrightarrow x = 30\) hoặc \(x = - 30\) (loại).

Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):

Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 3

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right) = f\left( {30} \right) = 510\).

Vậy để tiết kiệm chi phí xây dựng bể nhất, cần chọn các kích thước \(x = 30m\) và \(y = \frac{{900}}{{30}} = 30m\).

Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp giải

Bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm, tích phân, hoặc các ứng dụng của đạo hàm và tích phân trong thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:

Đạo hàm: Khái niệm, quy tắc tính đạo hàm của các hàm số cơ bản, đạo hàm của hàm hợp, đạo hàm cấp hai.
Tích phân: Khái niệm, tính chất, các phương pháp tính tích phân (đổi biến, tích phân từng phần).
Ứng dụng của đạo hàm: Khảo sát hàm số, tìm cực trị, giải phương trình, bất phương trình.
Ứng dụng của tích phân: Tính diện tích hình phẳng, thể tích vật thể.

Lời giải chi tiết bài 2 trang 20

Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 2. Tuy nhiên, dưới đây là một ví dụ minh họa về cách tiếp cận và giải quyết một bài toán tương tự:

Ví dụ minh họa:

Bài toán: Cho hàm số f(x) = x³ - 3x² + 2. Tìm các điểm cực trị của hàm số.

Lời giải:

Tính đạo hàm cấp nhất: f'(x) = 3x² - 6x
Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
Khảo sát dấu của đạo hàm cấp nhất:
- Khi x < 0: f'(x) > 0, hàm số đồng biến.
- Khi 0 < x < 2: f'(x) < 0, hàm số nghịch biến.
- Khi x > 2: f'(x) > 0, hàm số đồng biến.
Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.

Mẹo giải bài tập Toán 12 hiệu quả

Để học tốt môn Toán 12 và giải quyết các bài tập một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:

Nắm vững kiến thức cơ bản: Đây là nền tảng quan trọng nhất để giải quyết mọi bài toán.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn hiểu rõ hơn về các khái niệm và phương pháp giải.
Sử dụng sơ đồ tư duy: Sơ đồ tư duy giúp bạn hệ thống hóa kiến thức và dễ dàng ghi nhớ.
Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô, bạn bè hoặc tìm kiếm trên internet.
Sử dụng các công cụ hỗ trợ: Các công cụ như máy tính bỏ túi, phần mềm giải toán có thể giúp bạn tiết kiệm thời gian và công sức.

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

Tusach.vn là website cung cấp lời giải bài tập Toán 12, cùng với nhiều tài liệu học tập hữu ích khác. Chúng tôi luôn cập nhật nội dung mới nhất và cố gắng mang đến cho bạn trải nghiệm học tập tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu và lời giải bài tập Toán 12 nhé!

Chủ đề	Liên kết
Giải bài tập Toán 12 Chân trời sáng tạo	https://tusach.vn/toan-12-chan-troi-sang-tao
Chuyên đề học tập Toán 12	https://tusach.vn/chuyen-de-toan-12

Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp giải

Lời giải chi tiết bài 2 trang 20

Ví dụ minh họa:

Mẹo giải bài tập Toán 12 hiệu quả

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN