Giải bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 12 trang 23 trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi sẽ phân tích từng bước giải, giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết các bài toán tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là (p) nghìn đồng thì sẽ có ({rm{x}}) người mua vé xem biểu diễn, giữa (p) và ({rm{x}}) có mối liên hệ: (p = 500.{e^{ - 0,0005x}}). Đơn vị tổ chức nên bán vé với giá bao nhiêu thì đạt được doanh thu (tổng số tiền bán vé) cao nhất?
Đề bài
Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là \(p\) nghìn đồng thì sẽ có \({\rm{x}}\) người mua vé xem biểu diễn, giữa \(p\) và \({\rm{x}}\) có mối liên hệ: \(p = 500.{e^{ - 0,0005x}}\). Đơn vị tổ chức nên bán vé với giá bao nhiêu thì đạt được doanh thu (tổng số tiền bán vé) cao nhất?
Phương pháp giải - Xem chi tiết
• Biểu thị doanh thu thông qua \(p\) và \({\rm{x}}\).
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Doanh thu khi công ty bán được \(x\) vé với mỗi vé là \(p\) nghìn đồng là:
\(R\left( x \right) = p.x = 500.{e^{ - 0,0005x}}.x\) (triệu đồng)
Xét hàm số \(R\left( x \right) = 500.{e^{ - 0,0005x}}.x\) trên khoảng \(\left( {0; + \infty } \right)\).
Ta có:
\(\begin{array}{l}R'\left( x \right) = {\left( {500.{e^{ - 0,0005x}}} \right)^\prime }.x + 500.{e^{ - 0,0005x}}.{\left( x \right)^\prime } = 500.\left( { - 0,0005} \right).{e^{ - 0,0005x}}.x + 500.{e^{ - 0,0005x}}\\ = 500.{e^{ - 0,0005x}}\left( {1 - 0,0005x} \right)\end{array}\)
\(R'\left( x \right) = 0 \Leftrightarrow 500.{e^{ - 0,0005x}}\left( {1 - 0,0005x} \right) = 0 \Leftrightarrow x = 2000\).
Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):
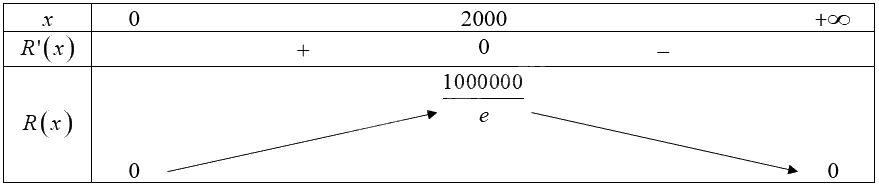
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left( {0; + \infty } \right)} R\left( x \right) = R\left( {2000} \right) = \frac{{1000000}}{e}\).
Vậy đơn vị tổ chức nên bán vé với giá \(p = 500.{e^{ - 0,0005.2000}} = \frac{{500}}{e} \approx 184\) nghìn đồng thì đạt được doanh thu (tổng số tiền bán vé) cao nhất.
Giải bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số, hoặc các bài toán liên quan đến cực trị của hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, quy tắc tính đạo hàm, và các phương pháp tìm cực trị.
Nội dung chi tiết bài 12 trang 23
Để cung cấp một lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 12. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và phân tích các đề thi, bài toán thường có dạng như sau:
Ví dụ minh họa (giả định):
Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy:
- Tìm đạo hàm f'(x).
- Tìm các điểm cực trị của hàm số.
- Khảo sát sự biến thiên của hàm số.
Lời giải chi tiết
Bước 1: Tìm đạo hàm f'(x)
Áp dụng quy tắc tính đạo hàm, ta có:
f'(x) = 3x2 - 6x
Bước 2: Tìm các điểm cực trị
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
⇔ 3x(x - 2) = 0
⇔ x = 0 hoặc x = 2
Vậy, hàm số có hai điểm cực trị là x = 0 và x = 2.
Bước 3: Khảo sát sự biến thiên của hàm số
Ta xét dấu của f'(x) trên các khoảng:
- Khoảng (-∞; 0): f'(x) > 0, hàm số đồng biến.
- Khoảng (0; 2): f'(x) < 0, hàm số nghịch biến.
- Khoảng (2; +∞): f'(x) > 0, hàm số đồng biến.
Từ đó, ta có thể kết luận:
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Mẹo giải nhanh và lưu ý quan trọng
Để giải nhanh các bài toán về khảo sát hàm số, bạn nên:
- Nắm vững các quy tắc tính đạo hàm.
- Sử dụng bảng xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến.
- Chú ý đến các điểm không xác định của đạo hàm.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác.
Tusach.vn - Đồng hành cùng bạn học Toán
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập Toán 12. Hãy truy cập website của chúng tôi để tìm hiểu thêm và nâng cao kiến thức của bạn!
| Chủ đề | Nội dung |
|---|---|
| Đạo hàm | Quy tắc tính đạo hàm, ứng dụng của đạo hàm |
| Cực trị | Tìm cực đại, cực tiểu của hàm số |
| Khảo sát hàm số | Xác định khoảng đồng biến, nghịch biến, điểm cực trị |
| Nguồn: Tusach.vn | |