Giải bài 3 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 3 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 3 trang 20 trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi sẽ phân tích từng bước giải, giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết các bài toán tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
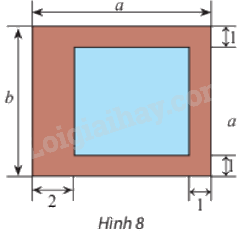
Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước có diện tích bằng 54 m2 và phần đường đi xung quanh với kích thước (đơn vị: m) như Hình 8. Bề mặt của lồng có chiều dài và chiều rộng bằng bao nhiêu để diện tích phần đường đi là bé nhất?
Đề bài
Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước có diện tích bằng 54 m2 và phần đường đi xung quanh với kích thước (đơn vị: m) như Hình 8. Bề mặt của lồng có chiều dài và chiều rộng bằng bao nhiêu để diện tích phần đường đi là bé nhất?
Phương pháp giải - Xem chi tiết
• Tìm mối quan hệ giữa \(a,b\), biểu thị diện tích phần đường đường đi thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Diện tích phần mặt nước là: \(\left( {a - 2 - 1} \right)\left( {b - 1 - 1} \right) = \left( {a - 3} \right)\left( {b - 2} \right)\) với \(a > 3,b > 2\).
Do phần mặt nước có diện tích bằng 54 m2 nên ta có:
\(\left( {a - 3} \right)\left( {b - 2} \right) = 54 \Leftrightarrow b - 2 = \frac{{54}}{{a - 3}} \Leftrightarrow b = \frac{{54}}{{a - 3}} + 2\)
Diện tích bể là: \(ab = a.\left( {\frac{{54}}{{a - 3}} + 2} \right) = \frac{{54a}}{{a - 3}} + 2a\).
Diện tích phần đường đi xung quanh là: \(S = \frac{{54a}}{{a - 3}} + 2a - 54 = \frac{{162}}{{a - 3}} + 2a\).
Xét hàm số \(S\left( a \right) = \frac{{162}}{{a - 3}} + 2a\) trên khoảng \(\left( {3; + \infty } \right)\).
Ta có: \(S'\left( a \right) = - \frac{{162}}{{{{\left( {a - 3} \right)}^2}}} + 2\)
\(S'\left( a \right) = 0 \Leftrightarrow - \frac{{162}}{{{{\left( {a - 3} \right)}^2}}} + 2 = 0 \Leftrightarrow {\left( {a - 3} \right)^2} = 81 \Leftrightarrow a = 12\) hoặc \({\rm{a}} = - 6\) (loại).
Bảng biến thiên của hàm số trên khoảng \(\left( {3; + \infty } \right)\):

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {3; + \infty } \right)} f\left( x \right) = f\left( {12} \right) = 42\).
Vậy diện tích phần đường đi \(S\) đạt giá trị nhỏ nhất khi \(a = 12\left( m \right)\) và \(b = \frac{{54}}{{12 - 3}} + 2 = 8\left( m \right)\).
Giải bài 3 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 3 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình, ví dụ như đạo hàm, tích phân, hoặc các bài toán về hình học không gian. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành bài tập một cách hiệu quả. Bài viết này sẽ đi sâu vào phân tích chi tiết từng phần của bài toán, cung cấp các ví dụ minh họa và hướng dẫn từng bước giải.
Nội dung chi tiết bài 3 trang 20
Để giải quyết bài 3 trang 20, trước tiên chúng ta cần xác định rõ yêu cầu của đề bài. Thông thường, đề bài sẽ yêu cầu chúng ta:
- Tính đạo hàm của hàm số.
- Tìm cực trị của hàm số.
- Giải phương trình hoặc bất phương trình.
- Tính tích phân.
- Xác định các yếu tố hình học (khoảng cách, góc, thể tích...).
Sau khi xác định yêu cầu, chúng ta sẽ áp dụng các công thức và phương pháp phù hợp để giải quyết bài toán. Dưới đây là một số phương pháp thường được sử dụng:
- Phương pháp đặt ẩn phụ: Sử dụng khi bài toán có cấu trúc phức tạp, việc đặt ẩn phụ sẽ giúp đơn giản hóa bài toán.
- Phương pháp biến đổi tương đương: Sử dụng để đưa bài toán về dạng quen thuộc, dễ giải quyết.
- Phương pháp sử dụng đạo hàm: Sử dụng để tìm cực trị, khoảng đơn điệu của hàm số.
- Phương pháp tích phân từng phần: Sử dụng để tính tích phân của các hàm số phức tạp.
Ví dụ minh họa
Giả sử bài 3 trang 20 yêu cầu chúng ta tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1. Chúng ta sẽ áp dụng quy tắc đạo hàm của tổng, hiệu và lũy thừa để tính đạo hàm:
f'(x) = 3x2 + 4x - 5
Lưu ý quan trọng
Khi giải bài tập Toán 12, đặc biệt là các bài tập trong Chuyên đề học tập, bạn cần:
- Nắm vững lý thuyết cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Kiểm tra lại kết quả sau khi giải xong.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm giải toán (nếu cần thiết).
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm:
- Giải bài tập trong sách giáo khoa và sách bài tập.
- Đề thi thử và đề thi chính thức các năm trước.
- Các bài viết hướng dẫn giải toán chi tiết và dễ hiểu.
Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu hữu ích khác và nâng cao kết quả học tập của bạn!
Bảng tổng hợp các công thức thường dùng
| Công thức | Mô tả |
|---|---|
| (u + v)' = u' + v' | Đạo hàm của tổng |
| (u - v)' = u' - v' | Đạo hàm của hiệu |
| (u * v)' = u'v + uv' | Đạo hàm của tích |