Giải mục 2 trang 9, 10, 11, 12 Chuyên đề học tập Toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải Mục 2 Trang 9, 10, 11, 12 Chuyên đề học tập Toán 12 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết Mục 2 trang 9, 10, 11, 12 Chuyên đề học tập Toán 12 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ hơn về nội dung bài học và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh.
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó?
Hoạt động 3
Trả lời câu hỏi Hoạt động 3 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó?
Phương pháp giải:
Trung bình = Tổng số vụ tai nạn / số buổi tối thứ Bảy
Lời giải chi tiết:
Có: \(0.10 + 1.20 + 2.23 + 3.25 + 4.15 + 7.5 = 236\) vụ vi phạm trong 98 buổi tối thứ Bảy
Vậy trung bình có \(\frac{{236}}{{98}} \approx 2,408\) vụ vi phạm trọng 98 buổi tối thứ Bảy
Câu hỏi
Trả lời câu hỏi trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Trở lại HĐ4. Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2. Tính độ lệch chuẩn của X và Y.
Phương pháp giải:
Áp dụng công thức tính độ lệch chuẩn
Lời giải chi tiết:
\(\begin{array}{l}E(X) = 4\\V(X) = {\left( {8 - 4} \right)^2}.\frac{1}{3} + {\left( {2 - 4} \right)^2}.\frac{2}{3} = 8\\ \Rightarrow \sigma (X) = \sqrt 8 \approx 2,828.\end{array}\)
\(\begin{array}{l}E(Y) = 4\\V\left( Y \right) = {\left( {5 - 4} \right)^2}.\frac{1}{2} + {\left( {3 - 4} \right)^2}.\frac{1}{2} = 1\\ \Rightarrow \sigma \left( Y \right) = 1\end{array}\)
Luyện tập 2
Trả lời câu hỏi Luyện tập 2 trang 10 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường vào tối thứ Bảy có thể là 0; 1; 2; 3; 4; 5 với các xác suất tương ứng là 0,1; 0,2; 0,25; 0,15 và 0,05. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường đó và tối thứ Bảy?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X
Bước 2: Tính kì vọng \(E(X)\) theo công thức
Lời giải chi tiết:
Gọi X là số vụ vi phạm Luật Giao thông đường bộ trên đoạn đường vào tối thứ Bảy. Khi đó, X là biến ngẫu nhiên rời rạc có bảng phân bố xác suất:

Ta có:
\(\;E(X) = 0,01 + 1.0,2 + 2.0,25 + 3.0,25 + 4.0,15 + 5.0,05 = 2,3\)
Vậy trên đoạn đường vào tối thứ Bảy có trung bình 2,3 vụ vi phạm Luật Giao thông đường bộ
Vận dụng 2
Trả lời câu hỏi Vận dụng 2 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Tiếp tục xét tình huống mở đầu, giả sử ở vòng 1 Minh chọn câu hỏi loại II.
a) Hỏi trung bình Minh nhận được bao nhiêu điểm?
b) Ở vòng 1 Minh nên chọn loại câu hỏi nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên Y.
Bước 2: Tính kì vọng \(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Giả sử ở vòng 1 Minh chọn câu hỏi loại II. Gọi Y là số điểm Minh nhận được.
Gọi A là biến cố “Minh trả lời đúng câu hỏi loại I” \( \Rightarrow P\left( A \right) = 0,8\)
B là biến cố “Minh trả lời đúng câu hỏi loại II”. \( \Rightarrow P\left( B \right) = 0,6\)
+ Nếu trả lời sai: Minh được 0 điểm. Cuộc chơi kết thúc tại đây
Khi đó, \(P\left( {Y = 0} \right) = P(\overline B ) = 1--P\left( B \right) = 1--0,6 = 0,4.\)
+ Nếu trả lời đúng Minh nhận 80 điểm và Minh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi loại I. Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi và số điểm với số điểm nhận được là 80 + 0 = 80 điểm. Theo giả thiết A và B là biến cố độc lập. Theo công thức nên xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 80} \right) = P(B\overline A ) = P\left( B \right)P(\overline A ) = \left( {0,6} \right)\left( {1--0,8} \right) = 0,12\)
+ Nếu trả lời đúng Minh nhận 80 điểm. Cuộc chơi kết thúc tại đây và Minh được 20 + 80 = 100 điểm. Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 100} \right) = P\left( {BA} \right) = P\left( B \right)P\left( A \right) = 0,6.{\rm{ }}0,8 = 0,48\)
Bảng phân bố xác suất của Y là:
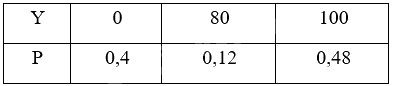
Ta có: \(E\left( Y \right) = 0.0,4 + 80.0,12 + 100.0,48 = 57,6\).
Vậy trung bình Minh được 57,6 điểm
b) Ta có \(E(X) = 54,4\), \(E(Y) = 57,6\). Ta thấy \(E(Y) > E(X)\) nên ở vòng 1, Minh nên chọn câu hỏi loại II.
Hoạt động 4
Trả lời câu hỏi Hoạt động 4 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Một nhà đầu tư xem xét hai phương án đầu tư. Với phương án 1 thì doanh thu một năm sẽ là 8 tỉ đồng hoặc 2 tỉ đồng với xác suất tương ứng là \(\frac{1}{3}\) và \(\frac{2}{3}\). Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau.
a) Hãy so sánh doanh thu trung bình của phương án 1 và phương án 2.
b) Nhà đầu tư nên chọn phương án nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X, Y.
Bước 2: Tính kì vọng \(E(X)\),\(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2
Ta có bảng phân bố xác suất của biến ngẫu nhiên X và Y

Khi đó, \(E(X) = 8.\frac{1}{3} + 2.\frac{2}{3} = 4\); \(E(Y) = 3.\frac{1}{2} + 5.\frac{1}{2} = 4\).
Ta thấy \(E(X) = E(Y)\) nên doanh thu trung bình của hai phương án bằng nhau.
b)
Phương án 1 nếu nhà đầu tư ưa mạo hiểm
Phương án 2 nếu nhà đầu tư muốn sự an toàn
Luyện tập 3
Trả lời câu hỏi Luyện tập 3 trang 12 Chuyên đề học tập Toán 12 Kết nối tri thức
Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:

a) Tính \(V(X)\) và \(\sigma (X)\) theo định nghĩa
b) Tính \(V(X)\) theo công thức (2).
Phương pháp giải:
Áp dụng các công thức để tính.
Lời giải chi tiết:
a)
\(E(X) = 0.0,16 + 1.0,18 + 2.0,25 + 3.0,28 + 4.0,13 = 2,04.\)
\(\begin{array}{l}V\left( X \right) = {\left( {0--2,04} \right)^2}.0,16 + {\left( {1--2,04} \right)^2}.0,18 + {\left( {2--2,04} \right)^2}.0,25 + {\left( {3--2,04} \right)^2}.0,28\\{\rm{ }} + {\left( {4--2,04} \right)^2}.0,13 = 1,6184.\\ \Rightarrow \sigma \left( X \right) = \sqrt {1,6184} \approx 1,2722\end{array}\)
b) \(V\left( X \right) = {0^2}.0,16 + {1^2}.0,18 + {2^2}.0,25 + {3^2}.0,28 + {4^2}.0,13--{\left( {2,04} \right)^2} = 1,6184.\)
- Hoạt động 3
- Luyện tập 2
- Vận dụng 2
- Hoạt động 4
- Câu hỏi
- Luyện tập 3
Trả lời câu hỏi Hoạt động 3 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó?
Phương pháp giải:
Trung bình = Tổng số vụ tai nạn / số buổi tối thứ Bảy
Lời giải chi tiết:
Có: \(0.10 + 1.20 + 2.23 + 3.25 + 4.15 + 7.5 = 236\) vụ vi phạm trong 98 buổi tối thứ Bảy
Vậy trung bình có \(\frac{{236}}{{98}} \approx 2,408\) vụ vi phạm trọng 98 buổi tối thứ Bảy
Trả lời câu hỏi Luyện tập 2 trang 10 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường vào tối thứ Bảy có thể là 0; 1; 2; 3; 4; 5 với các xác suất tương ứng là 0,1; 0,2; 0,25; 0,15 và 0,05. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường đó và tối thứ Bảy?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X
Bước 2: Tính kì vọng \(E(X)\) theo công thức
Lời giải chi tiết:
Gọi X là số vụ vi phạm Luật Giao thông đường bộ trên đoạn đường vào tối thứ Bảy. Khi đó, X là biến ngẫu nhiên rời rạc có bảng phân bố xác suất:

Ta có:
\(\;E(X) = 0,01 + 1.0,2 + 2.0,25 + 3.0,25 + 4.0,15 + 5.0,05 = 2,3\)
Vậy trên đoạn đường vào tối thứ Bảy có trung bình 2,3 vụ vi phạm Luật Giao thông đường bộ
Trả lời câu hỏi Vận dụng 2 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Tiếp tục xét tình huống mở đầu, giả sử ở vòng 1 Minh chọn câu hỏi loại II.
a) Hỏi trung bình Minh nhận được bao nhiêu điểm?
b) Ở vòng 1 Minh nên chọn loại câu hỏi nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên Y.
Bước 2: Tính kì vọng \(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Giả sử ở vòng 1 Minh chọn câu hỏi loại II. Gọi Y là số điểm Minh nhận được.
Gọi A là biến cố “Minh trả lời đúng câu hỏi loại I” \( \Rightarrow P\left( A \right) = 0,8\)
B là biến cố “Minh trả lời đúng câu hỏi loại II”. \( \Rightarrow P\left( B \right) = 0,6\)
+ Nếu trả lời sai: Minh được 0 điểm. Cuộc chơi kết thúc tại đây
Khi đó, \(P\left( {Y = 0} \right) = P(\overline B ) = 1--P\left( B \right) = 1--0,6 = 0,4.\)
+ Nếu trả lời đúng Minh nhận 80 điểm và Minh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi loại I. Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi và số điểm với số điểm nhận được là 80 + 0 = 80 điểm. Theo giả thiết A và B là biến cố độc lập. Theo công thức nên xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 80} \right) = P(B\overline A ) = P\left( B \right)P(\overline A ) = \left( {0,6} \right)\left( {1--0,8} \right) = 0,12\)
+ Nếu trả lời đúng Minh nhận 80 điểm. Cuộc chơi kết thúc tại đây và Minh được 20 + 80 = 100 điểm. Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 100} \right) = P\left( {BA} \right) = P\left( B \right)P\left( A \right) = 0,6.{\rm{ }}0,8 = 0,48\)
Bảng phân bố xác suất của Y là:
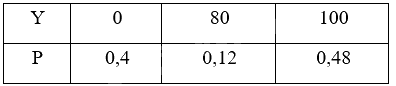
Ta có: \(E\left( Y \right) = 0.0,4 + 80.0,12 + 100.0,48 = 57,6\).
Vậy trung bình Minh được 57,6 điểm
b) Ta có \(E(X) = 54,4\), \(E(Y) = 57,6\). Ta thấy \(E(Y) > E(X)\) nên ở vòng 1, Minh nên chọn câu hỏi loại II.
Trả lời câu hỏi Hoạt động 4 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Một nhà đầu tư xem xét hai phương án đầu tư. Với phương án 1 thì doanh thu một năm sẽ là 8 tỉ đồng hoặc 2 tỉ đồng với xác suất tương ứng là \(\frac{1}{3}\) và \(\frac{2}{3}\). Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau.
a) Hãy so sánh doanh thu trung bình của phương án 1 và phương án 2.
b) Nhà đầu tư nên chọn phương án nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X, Y.
Bước 2: Tính kì vọng \(E(X)\),\(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2
Ta có bảng phân bố xác suất của biến ngẫu nhiên X và Y

Khi đó, \(E(X) = 8.\frac{1}{3} + 2.\frac{2}{3} = 4\); \(E(Y) = 3.\frac{1}{2} + 5.\frac{1}{2} = 4\).
Ta thấy \(E(X) = E(Y)\) nên doanh thu trung bình của hai phương án bằng nhau.
b)
Phương án 1 nếu nhà đầu tư ưa mạo hiểm
Phương án 2 nếu nhà đầu tư muốn sự an toàn
Trả lời câu hỏi trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Trở lại HĐ4. Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2. Tính độ lệch chuẩn của X và Y.
Phương pháp giải:
Áp dụng công thức tính độ lệch chuẩn
Lời giải chi tiết:
\(\begin{array}{l}E(X) = 4\\V(X) = {\left( {8 - 4} \right)^2}.\frac{1}{3} + {\left( {2 - 4} \right)^2}.\frac{2}{3} = 8\\ \Rightarrow \sigma (X) = \sqrt 8 \approx 2,828.\end{array}\)
\(\begin{array}{l}E(Y) = 4\\V\left( Y \right) = {\left( {5 - 4} \right)^2}.\frac{1}{2} + {\left( {3 - 4} \right)^2}.\frac{1}{2} = 1\\ \Rightarrow \sigma \left( Y \right) = 1\end{array}\)
Trả lời câu hỏi Luyện tập 3 trang 12 Chuyên đề học tập Toán 12 Kết nối tri thức
Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:

a) Tính \(V(X)\) và \(\sigma (X)\) theo định nghĩa
b) Tính \(V(X)\) theo công thức (2).
Phương pháp giải:
Áp dụng các công thức để tính.
Lời giải chi tiết:
a)
\(E(X) = 0.0,16 + 1.0,18 + 2.0,25 + 3.0,28 + 4.0,13 = 2,04.\)
\(\begin{array}{l}V\left( X \right) = {\left( {0--2,04} \right)^2}.0,16 + {\left( {1--2,04} \right)^2}.0,18 + {\left( {2--2,04} \right)^2}.0,25 + {\left( {3--2,04} \right)^2}.0,28\\{\rm{ }} + {\left( {4--2,04} \right)^2}.0,13 = 1,6184.\\ \Rightarrow \sigma \left( X \right) = \sqrt {1,6184} \approx 1,2722\end{array}\)
b) \(V\left( X \right) = {0^2}.0,16 + {1^2}.0,18 + {2^2}.0,25 + {3^2}.0,28 + {4^2}.0,13--{\left( {2,04} \right)^2} = 1,6184.\)
Giải Mục 2 Trang 9, 10, 11, 12 Chuyên đề học tập Toán 12 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 12 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề. Việc giải các bài tập trang 9, 10, 11, 12 không chỉ giúp học sinh củng cố lý thuyết mà còn rèn luyện khả năng áp dụng kiến thức vào thực tế.
Nội dung chính của Mục 2 (tùy theo chuyên đề cụ thể)
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định chủ đề chính mà nó đề cập đến. Ví dụ:
- Nếu Mục 2 nói về Đạo hàm: Các bài tập sẽ xoay quanh việc tính đạo hàm của các hàm số, ứng dụng đạo hàm để khảo sát hàm số, tìm cực trị, và giải các bài toán liên quan đến tối ưu hóa.
- Nếu Mục 2 nói về Tích phân: Các bài tập sẽ tập trung vào việc tính tích phân, ứng dụng tích phân để tính diện tích, thể tích, và giải các bài toán vật lý.
- Nếu Mục 2 nói về Số phức: Các bài tập sẽ liên quan đến các phép toán trên số phức, phương trình bậc hai với hệ số phức, và biểu diễn hình học của số phức.
Hướng dẫn giải chi tiết các bài tập trang 9, 10, 11, 12
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 2:
Bài 1 (Trang 9):
(Giả sử bài tập là tính đạo hàm của hàm số f(x) = x2 + 2x - 1)
Lời giải:
Áp dụng quy tắc đạo hàm của tổng và đạo hàm của hàm số lũy thừa, ta có:
f'(x) = 2x + 2
Bài 2 (Trang 10):
(Giả sử bài tập là tìm cực trị của hàm số f(x) = x3 - 3x2 + 2)
Lời giải:
- Tính đạo hàm bậc nhất: f'(x) = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được x = 0 và x = 2
- Tính đạo hàm bậc hai: f''(x) = 6x - 6
- Kiểm tra dấu của đạo hàm bậc hai tại các điểm dừng:
- f''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0
- f''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2
- Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong Mục 2 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Nắm vững các công thức và định lý: Điều này giúp bạn tiết kiệm thời gian và tránh sai sót.
- Phân tích kỹ đề bài: Xác định rõ yêu cầu của đề bài và các dữ kiện đã cho.
- Sử dụng các phương pháp giải phù hợp: Tùy thuộc vào từng bài tập, bạn có thể sử dụng các phương pháp giải khác nhau.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 12:
- Sách bài tập Toán 12
- Các trang web học Toán trực tuyến
- Các video hướng dẫn giải Toán trên YouTube
Tusach.vn hy vọng rằng với những hướng dẫn chi tiết và hữu ích này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Mục 2 trang 9, 10, 11, 12 Chuyên đề học tập Toán 12 - Kết nối tri thức. Chúc các em học tốt!