Giải bài 2.7 trang 42 Chuyên đề học tập Toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 2.7 trang 42 Chuyên đề học tập Toán 12 - Kết nối tri thức
Bài 2.7 trang 42 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Người ta muốn kéo một đường dây điện tử nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C
Đề bài
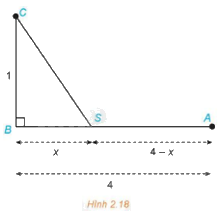
Người ta muốn kéo một đường dây điện tử nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C (Hình 2.18). Tìm vị trí điểm S sao cho chi phí kéo đường dây là nhỏ nhất.
Phương pháp giải - Xem chi tiết
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết
Đặt \(BS = x{\rm{ }}(m)\)\((0 \le x \le 4)\). Khi đó, \(SA = 4 - x;CS = \sqrt {1 + {x^2}} \)
Khi đó, chi phí cần bỏ ra là: \(f(x) = 5{\rm{ }}000\sqrt {1 + {x^2}} + 3{\rm{ }}000(4 - x)\), \(x \in \left[ {0;4} \right]\)
\(f'(x) = \frac{{5{\rm{ }}000x}}{{\sqrt {1 + {x^2}} }} - 3{\rm{ }}000\)
\(f'(x) = 0 \Leftrightarrow 3\sqrt {1 + {x^2}} = 5x \Leftrightarrow x = \frac{3}{4}\)
Ta có \(f(0) = 17{\rm{ }}000;f\left( {\frac{3}{4}} \right) = 16{\rm{ }}000;f(4) \approx 20{\rm{ }}616\). Ta thấy GTNN ứng với \(x = \frac{3}{4}\).
Vậy điểm S trên bờ biển cần tìm cách A một khoảng \(4 - \frac{3}{4} = \frac{{13}}{4}(km)\).
Giải bài 2.7 trang 42 Chuyên đề học tập Toán 12 - Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu
Bài 2.7 trang 42 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tối ưu hóa. Để giải bài này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
- Xác định hàm số mục tiêu: Đọc kỹ đề bài để xác định hàm số cần tối ưu hóa (ví dụ: hàm số biểu diễn diện tích, chi phí, lợi nhuận,...).
- Tìm tập xác định của hàm số: Xác định miền giá trị của biến số trong bài toán.
- Tính đạo hàm của hàm số: Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm cấp nhất của hàm số.
- Tìm điểm dừng của hàm số: Giải phương trình đạo hàm bằng 0 để tìm các điểm dừng.
- Xác định khoảng đơn điệu của hàm số: Xét dấu đạo hàm trên các khoảng xác định để xác định khoảng hàm số đồng biến và nghịch biến.
- Tìm giá trị lớn nhất và nhỏ nhất của hàm số: Dựa vào khoảng đơn điệu và giá trị tại các điểm dừng để tìm giá trị lớn nhất và nhỏ nhất của hàm số trên tập xác định.
- Kết luận: Trả lời câu hỏi của bài toán dựa trên kết quả tìm được.
Phân tích chi tiết bài toán 2.7 trang 42
Để minh họa, chúng ta cùng xem xét một ví dụ cụ thể. Giả sử bài toán yêu cầu tìm kích thước của một mảnh đất hình chữ nhật có diện tích cho trước sao cho chu vi nhỏ nhất.
Bước 1: Gọi chiều dài và chiều rộng của mảnh đất lần lượt là x và y. Diện tích mảnh đất là xy = A (A là hằng số). Hàm số cần tối ưu hóa là chu vi P = 2(x + y).
Bước 2: Tập xác định của hàm số là x > 0 và y > 0.
Bước 3: Từ xy = A, ta có y = A/x. Thay vào hàm chu vi, ta được P(x) = 2(x + A/x).
Bước 4: Tính đạo hàm P'(x) = 2(1 - A/x2). Giải phương trình P'(x) = 0, ta được x2 = A, suy ra x = √A (do x > 0).
Bước 5: Xét dấu P'(x). Khi x < √A, P'(x) < 0 (hàm nghịch biến). Khi x > √A, P'(x) > 0 (hàm đồng biến). Vậy hàm số đạt giá trị nhỏ nhất tại x = √A.
Bước 6: Khi x = √A, y = A/√A = √A. Vậy mảnh đất có chu vi nhỏ nhất là hình vuông có cạnh √A.
Bước 7: Kết luận: Kích thước của mảnh đất hình chữ nhật có diện tích A và chu vi nhỏ nhất là hình vuông có cạnh √A.
Mẹo giải bài tập đạo hàm hiệu quả
- Nắm vững các quy tắc tính đạo hàm: Đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng công cụ hỗ trợ: Máy tính bỏ túi có chức năng tính đạo hàm có thể giúp kiểm tra kết quả và tiết kiệm thời gian.
- Hiểu rõ bản chất của bài toán: Đừng chỉ học thuộc công thức mà hãy cố gắng hiểu rõ ý nghĩa của các khái niệm và ứng dụng của đạo hàm.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn luôn đồng hành cùng các bạn học sinh trong quá trình học tập môn Toán 12. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các bài tập luyện tập để giúp các bạn đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!