Giải bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức

Tusach.vn xin giới thiệu bài giải chi tiết bài 1.3 trang 13 Chuyên đề học tập Toán 12 Kết nối tri thức. Bài viết này cung cấp đáp án, lời giải chi tiết và phương pháp giải bài tập một cách dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác và hữu ích nhất cho các em học sinh.

Một túi gồm các tấm thẻ giống hệt nhau chỉ khác màu, trong đó có 10 tấm thẻ màu đỏ và 6 tấm thẻ màu xanh. Rút ngẫu nhiên đồng thời ra 3 tấm thẻ từ trong túi. a) Gọi X là số thẻ đỏ trong ba thẻ rút ra. Lập bảng phân bố xác suất của X. Tính (Eleft( X right).) b) Giả sử rút mỗi tấm thẻ màu đỏ được 5 điểm và rút mỗi tấm thẻ màu xanh được 8 điểm. Gọi Y là số điểm thu được sau khi rút 3 tấm thẻ từ trong túi. Lập bảng phân bố xác suất của Y.

Đề bài

Một túi gồm các tấm thẻ giống hệt nhau chỉ khác màu, trong đó có 10 tấm thẻ màu đỏ và 6 tấm thẻ màu xanh. Rút ngẫu nhiên đồng thời ra 3 tấm thẻ từ trong túi.

a) Gọi X là số thẻ đỏ trong ba thẻ rút ra. Lập bảng phân bố xác suất của X. Tính \(E\left( X \right).\)

b) Giả sử rút mỗi tấm thẻ màu đỏ được 5 điểm và rút mỗi tấm thẻ màu xanh được 8 điểm.

Gọi Y là số điểm thu được sau khi rút 3 tấm thẻ từ trong túi. Lập bảng phân bố xác suất của Y.

Phương pháp giải - Xem chi tiết Giải bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức 1

Bước 1: Tính xác suất của các biến cố

Bước 2: Lập bảng phân bố xác suất

Bước 3: Tính \(E\left( X \right)\)theo công thức

Lời giải chi tiết

X là số thẻ đỏ trong ba thẻ rút ra \( \Rightarrow \) Giá trị của X thuộc tập {0; 1; 2; 3}.

Số kết quả có thể là: \(C_{16}^3 = 560\).

Biến cố \(\left\{ {X = 0} \right\}\): “Rút được 3 thẻ xanh”. \( \Rightarrow P\left( {X = 0} \right) = \frac{{C_6^3}}{{C_{16}^3}} = \frac{2}{{56}}\)

Biến cố \(\left\{ {X = 1} \right\}:\) “Rút được 1 thẻ đỏ và 2 thẻ xanh”. \( \Rightarrow P\left( {X = 1} \right) = \frac{{C_{10}^1.C_6^2}}{{C_{16}^3}} = \frac{{15}}{{56}}\)

Biến cố \(\left\{ {X = 2} \right\}:\) “Rút được 2 thẻ đỏ và 1 thẻ xanh”. \( \Rightarrow P\left( {X = 2} \right) = \frac{{C_{10}^2.C_6^1}}{{C_{16}^3}} = \frac{{27}}{{56}}\)

Biến cố \(\left\{ {X = 3} \right\}:\) “Rút được 3 thẻ đỏ”. \( \Rightarrow P\left( {X = 3} \right) = \frac{{C_{10}^3}}{{C_{16}^3}} = \frac{{12}}{{56}}\)

Bảng phân bố xác suất của X là

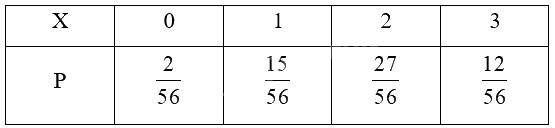
Giải bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức 2

Ta có: \(E(X) = 0.\frac{2}{{56}} + 1.\frac{{15}}{{56}} + 2.\frac{{27}}{{56}} + 3.\frac{{12}}{{56}} = 1,875\).

b) Y là số điểm thu được sau khi rút 3 tấm thẻ từ trong túi

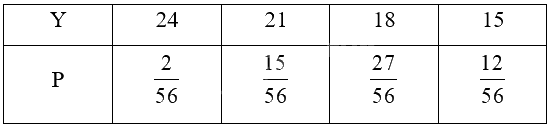
\( \Rightarrow \) Giá trị của Y thuộc tập {24; 21; 18; 15}

Ta có:

\(\begin{array}{l}P\left( {Y = 24} \right) = P\left( {X = 0} \right) = \frac{2}{{56}};P\left( {Y = 21} \right) = P\left( {X = 1} \right) = \frac{{15}}{{56}}\\P\left( {Y = 18} \right) = P\left( {X = 2} \right) = \frac{{27}}{{56}};P\left( {Y = 15} \right) = P\left( {X = 3} \right) = \frac{{12}}{{56}}\end{array}\)

Bảng phân bố xác suất của Y là

Giải bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức 3

Giải bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức: Tổng quan

Bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.

Nội dung bài tập 1.3 trang 13

Bài tập 1.3 thường bao gồm các dạng bài sau:

Tính đạo hàm của hàm số tại một điểm.
Tìm đạo hàm của hàm số.
Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.
Khảo sát hàm số bằng đạo hàm.

Lời giải chi tiết bài 1.3 trang 13

Để giải bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức, chúng ta cần thực hiện các bước sau:

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần tính đạo hàm hoặc khảo sát.
Áp dụng quy tắc tính đạo hàm: Sử dụng các quy tắc tính đạo hàm đã học (đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...) để tính đạo hàm của hàm số.
Rút gọn biểu thức: Rút gọn biểu thức đạo hàm để có được kết quả cuối cùng.
Kiểm tra lại kết quả: Kiểm tra lại kết quả bằng cách thay các giá trị cụ thể vào hàm số và đạo hàm để đảm bảo tính chính xác.

Ví dụ minh họa

Bài toán: Tính đạo hàm của hàm số f(x) = x² + 2x - 1.

Lời giải:

f'(x) = 2x + 2

Mẹo giải bài tập đạo hàm

Nắm vững các quy tắc tính đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính cầm tay để kiểm tra kết quả.
Tham khảo các tài liệu tham khảo và bài giải trên mạng.

Tài liệu tham khảo hữu ích

Để học tốt môn Toán 12 và giải các bài tập đạo hàm, các em có thể tham khảo các tài liệu sau:

Sách giáo khoa Toán 12 - Kết nối tri thức.
Sách bài tập Toán 12 - Kết nối tri thức.
Các trang web học Toán trực tuyến uy tín như Tusach.vn.
Các video bài giảng Toán 12 trên YouTube.

Kết luận

Bài 1.3 trang 13 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm. Hy vọng với bài giải chi tiết và các lời khuyên trên, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán 12.

Quy tắc	Công thức
Đạo hàm của hằng số	(c)' = 0
Đạo hàm của xⁿ	(xⁿ)' = nx^n-1
Đạo hàm của u + v	(u + v)' = u' + v'
Bảng quy tắc đạo hàm cơ bản

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN

Giới Thiệu
Chính Sách Bảo Mật
Liên Hệ
Blog
Email: Taisachebook@gmail.com