Giải bài 2.5 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 2.5 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức
Bài 2.5 trang 33 Chuyên đề học tập Toán 12 thuộc chương trình Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tính đơn điệu của hàm số.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Một hãng bán gà rán nghiên cứu thấy rằng để làm ra món gà rán có chất lượng tốt nhất thì thức ăn cho gà cần được bổ sung thêm 4 loại vitamin V1, V2, V3 và V4. Tổng lượng vitamin tối thiểu phải bổ sung cho mỗi 100 gam thức ăn cho gà là: V1 cần 50 đơn vị, V2 cần 100 đơn vị, V3 cần 60 đơn vị và V4 cần 180 đơn vị. Có hai loại thức ăn S1 và S2 cung cấp 4 loại vitamin này. Loại S1 có giá 720 đồng một gam và mỗi gam S1 có chứa 5 đơn vị V1, 25 đơn vị V2, 10 đơn vị V3 và 35 đơn vị V4. Loại S2 có giá 960
Đề bài
Một hãng bán gà rán nghiên cứu thấy rằng để làm ra món gà rán có chất lượng tốt nhất thì thức ăn cho gà cần được bổ sung thêm 4 loại vitamin V1, V2, V3 và V4. Tổng lượng vitamin tối thiểu phải bổ sung cho mỗi 100 gam thức ăn cho gà là: V1 cần 50 đơn vị, V2 cần 100 đơn vị, V3 cần 60 đơn vị và V4 cần 180 đơn vị. Có hai loại thức ăn S1 và S2 cung cấp 4 loại vitamin này. Loại S1 có giá 720 đồng một gam và mỗi gam S1 có chứa 5 đơn vị V1, 25 đơn vị V2, 10 đơn vị V3 và 35 đơn vị V4. Loại S2 có giá 960 đồng một gam và mỗi gam S2 có chứa 25 đơn vị V1, 10 đơn vị V2, 10 đơn vị V3 và 20 đơn vị V4. Hỏi cần phải thêm vào 100 gam thức ăn cho gà mỗi loại S1 và S2 bao nhiêu gam để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà.
Phương pháp giải - Xem chi tiết
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết
Gọi x, y lần lượt là số gam thức ăn loại S1 và S2 cần thêm vào 100 gam thức ăn cho gà.
Chi phí mua thức ăn là: F(x; y) = 720x + 960y (đồng).
Ta có hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\5x + 25y \ge 50\\25x + 10y \ge 100\\10x + 10y \ge 60\\35x + 20y \ge 180\end{array} \right.\)
Miền nghiệm của hệ bất phương trình này là miền tô màu, không bị chặn như hình vẽ dưới đây:
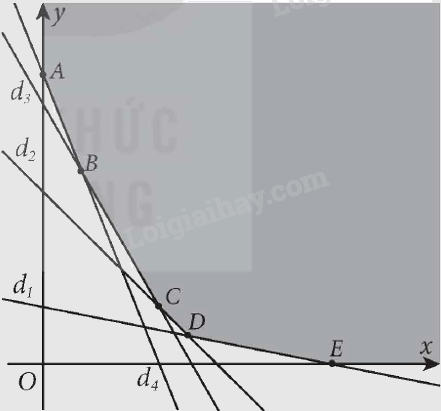
Các điểm cực biên là: A(0; 10),\(B\left( {\frac{4}{3};\frac{{20}}{3}} \right)\), C(4; 2), D(5; 1), E(10; 0).
F(0; 10) = 720.0 + 960.10 = 9 600;
\(F\left( {\frac{4}{3};\frac{{20}}{3}} \right) = 720 \cdot \frac{4}{3} + \;960 \cdot \frac{{20}}{3} = 7360;\)
F(4; 2) = 720.4 + 960.2 = 4 800;
F(5; 1) = 720.5 + 960.1 = 4 560;
F(10; 0) = 720.10 + 960.0 = 7 200.
Do đó giá trị nhỏ nhất của F(x; y) bằng 4 560 tại điểm cực biên D(5; 1).
Vậy cần phải thêm vào 100 gam thức ăn cho gà là 5 g loại S1 và 1 g loại S2 để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà.
Giải bài 2.5 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức: Hướng dẫn chi tiết
Bài 2.5 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc xét tính đơn điệu của hàm số. Dưới đây là hướng dẫn giải chi tiết bài tập này:
Đề bài:
Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
- Tính đạo hàm f'(x):
- Tìm các điểm cực trị:
- Xét dấu f'(x):
- Kết luận:
- Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Hàm số nghịch biến trên khoảng (0; 2).
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Các kiến thức liên quan cần nắm vững:
- Đạo hàm: Định nghĩa, các quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Tính đơn điệu của hàm số: Mối liên hệ giữa dấu của đạo hàm và tính đơn điệu của hàm số.
- Điểm cực trị: Điều kiện để hàm số có cực đại, cực tiểu.
Mẹo giải bài tập:
Khi giải các bài tập về tính đơn điệu của hàm số, bạn nên:
- Tính đạo hàm f'(x) một cách chính xác.
- Tìm các điểm cực trị bằng cách giải phương trình f'(x) = 0.
- Lập bảng xét dấu f'(x) để xác định khoảng đồng biến, nghịch biến của hàm số.
- Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.
Bài tập tương tự:
Để luyện tập thêm, bạn có thể giải các bài tập tương tự trong sách giáo khoa và sách bài tập Toán 12 Kết nối tri thức. Ngoài ra, bạn có thể tìm kiếm các bài tập trực tuyến trên các trang web học tập uy tín.
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một trang web cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm:
- Giải bài tập sách giáo khoa
- Giải bài tập sách bài tập
- Đề thi thử
- Bài giảng video
Hãy truy cập Tusach.vn để học tập và ôn luyện Toán 12 hiệu quả!