Trả lời câu hỏi Hoạt động 1 trang 24 Chuyên đề học tập Toán 12 Kết nối tri thức
Trong bài toán mở đầu, gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.
a) Kí hiệu F(x; y) là lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II. Viết biểu thức tính F(x; y) theo x và y.
b) Lập hệ bất phương trình bậc nhất hai ẩn ràng buộc x và y thỏa mãn yêu cầu của bài toán.
c) Biểu diễn trên mặt phẳng toạ độ để thấy rằng miền nghiệm của hệ bất phương trình tìm được trong ý b là một miền tứ giác. Tìm toạ độ các đỉnh của miền tứ giác này.
d) Tính giá trị của F(x; y) tại các đỉnh của miền tứ giác tìm được trong ý b, từ đó dự đoán về mức lợi nhuận cao nhất.
Phương pháp giải:
Dựa trên dữ kiện đề bài và các kiến thức đã học về bất phương trình bậc nhất hai ẩn, hệ bất phương trình bậc nhất hai ẩn
Lời giải chi tiết:
a) Lợi nhuận đem lại từ x kg sản phẩm loại I là 40x nghìn đồng.
Lợi nhuận đem lại từ y kg sản phẩm loại II là 30y nghìn đồng.
Khi đó, \(F\left( {x;y} \right) = 40x + 30y\) (nghìn đồng).
b) Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).
Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).
Vì xí nghiệp có 200 kg nguyên liệu và tối đa 1 200 giờ làm việc nên ta có:
\(\left\{ \begin{array}{l}2x + 4y \le 200\\30x + 15y \le 1{\rm{ }}200\\x \ge 0,y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y \le 100\\2x + y \le 80\\x \ge 0,y \ge 0\end{array} \right.\)
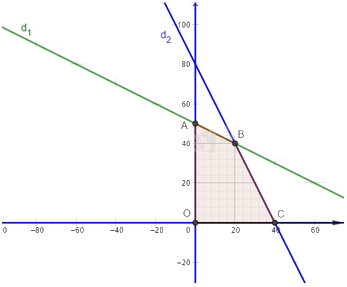
c) Miền nghiệm của hệ bất phương trình trong ý b là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d1: x + 2y = 100 và đường thẳng d2: 2x + y = 80.
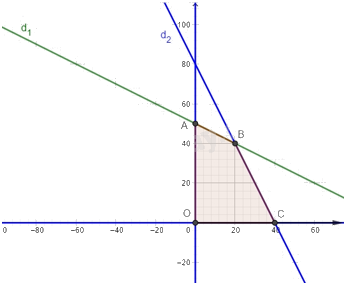
A là giao điểm của đường thẳng d1 với trục tung nên A(0; 50).
B là giao điểm của hai đường thẳng d1 và d2 nên B(20; 40).
C là giao điểm của đường thẳng d2 với trục hoành nên C(40; 0).
Vậy các đỉnh của miền nghiệm là: O(0; 0), A(0; 50), B(20; 40), C(40; 0).
d) Ta có:
\(\begin{array}{*{20}{l}}{F\left( {0;0} \right) = 40.0 + 30.0 = 0}\\{F\left( {0;50} \right) = 40.0 + 30.50 = 1{\rm{ }}500}\\{F\left( {20;40} \right) = 40.20 + 30.40 = 2{\rm{ }}000}\\{F\left( {40;0} \right) = {\rm{ }}40.40 + 30.0 = 1{\rm{ }}600}\end{array}\)
Dự đoán mức lợi nhuận cao nhất là 2 000 nghìn đồng, hay 2 triệu đồng.