Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề 2. Ứng dụng toán học để giải quyết một số bài toán tối ưu
Bài 3. Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính

Giải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức

Giải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức

Bài 2.2 trang 32 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hãy cùng Tusach.vn khám phá lời giải chi tiết bài tập này ngay nhé!

Một cơ sở sản xuất hai loại sữa chua X và Y. Nguyên liệu chính để sản xuất hai loại sữa chua này dâu tây, sữa và đường. Để sản xuất một đơn vị sữa chua X và một đơn vị sữa chua Y cần lượng nguyên liệu như trong bảng: Nguồn nguyên liệu dự trữ dâu tây, sữa và đường lần lượt là 1,2 tấn; 0,8 tấn và 0,3 tấn. Giá bán mỗi đơn vị sữa chua X và Y lần lượt là 800 nghìn đồng và 1,2 triệu đồng. Cơ sở sản xuất cần sản xuất bao nhiêu đơn vị sữa chua X và Y để lợi nhuận thu được là lớn nhất?

Đề bài

Một cơ sở sản xuất hai loại sữa chua X và Y. Nguyên liệu chính để sản xuất hai loại sữa chua này dâu tây, sữa và đường. Để sản xuất một đơn vị sữa chua X và một đơn vị sữa chua Y cần lượng nguyên liệu như trong bảng:

Giải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức 1

Nguồn nguyên liệu dự trữ dâu tây, sữa và đường lần lượt là 1,2 tấn; 0,8 tấn và 0,3 tấn. Giá bán mỗi đơn vị sữa chua X và Y lần lượt là 800 nghìn đồng và 1,2 triệu đồng. Cơ sở sản xuất cần sản xuất bao nhiêu đơn vị sữa chua X và Y để lợi nhuận thu được là lớn nhất?

Phương pháp giải - Xem chi tiếtGiải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức 2

Phương án tối ưu của bài toán đạt được tị vô số điểm trên mièn chấp nhận được.

Lời giải chi tiết

Gọi x và y lần lượt là số đơn vị sữa chua X và Y cần sản xuất.

Lợi nhuận thu được là: 0,8x + 1,2y (triệu đồng).

Ta có hệ bất phương trình sau:

\(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 300\\2x + 3y \le 1{\rm{ }}200\\2x + y \le 800\end{array} \right.\)

Miền nghiệm của hệ bất phương trình này là miền tứ giác ABCD được tô màu như hình vẽ dưới đây:

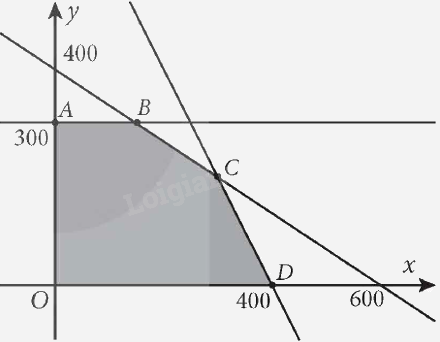
Giải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức 3

Các điểm cực biên là: O(0; 0), A(0; 300), B(150; 300), C(300; 200), D(400; 0).

Ta có đường thẳng BC có phương trình là 2x + 3y = 1 200, nên với mọi điểm M(x; y) thuộc đường thẳng BC ta đều có:

F(x; y) = 0,8x + 1,2y = 0,4(2x+ 3y) = 0,4 . 1 200 = 480.

Vậy biểu thức F(x; y) đạt giá trị lớn nhất bằng 480 tại mọi điểm M(x; y) thuộc đoạn thẳng BC. Như vậy bài toán có vô số phương án tối ưu.

Vậy cơ sở sản xuất cần sản xuất x đơn vị sữa chua X và \(y = 400 - \frac{2}{3}x\) đơn vị sữa chua Y với 150 ≤ x ≤ 300 thì lợi nhuận thu được là lớn nhất.

Giải bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu

Bài 2.2 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài toán yêu cầu học sinh vận dụng kiến thức về đạo hàm để tìm cực trị của hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:

  1. Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
  2. Tính đạo hàm cấp một: Sử dụng các quy tắc đạo hàm để tính đạo hàm f'(x) của hàm số.
  3. Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng không. Đây là các điểm có khả năng là cực trị.
  4. Khảo sát dấu của đạo hàm: Lập bảng xét dấu f'(x) trên các khoảng xác định bởi các điểm dừng.
  5. Kết luận về cực trị: Dựa vào bảng xét dấu, xác định các điểm cực đại, cực tiểu của hàm số.

Lời giải chi tiết bài 2.2 trang 32

Đề bài: (Giả sử đề bài cụ thể của bài 2.2 được đưa ra ở đây. Ví dụ: Tìm cực đại, cực tiểu của hàm số y = x3 - 3x2 + 2)

Giải:

  • Tập xác định: Hàm số y = x3 - 3x2 + 2 có tập xác định là D = ℝ.
  • Đạo hàm cấp một: y' = 3x2 - 6x
  • Điểm dừng: Giải phương trình 3x2 - 6x = 0, ta được x = 0 hoặc x = 2.
  • Bảng xét dấu:
    x-∞02+∞
    y'+-+
    y↗↘↗
  • Kết luận: Hàm số đạt cực đại tại x = 0, yCĐ = 2 và đạt cực tiểu tại x = 2, yCT = -2.

Mở rộng và lưu ý

Trong quá trình giải bài tập về cực trị hàm số, cần lưu ý:

  • Kiểm tra kỹ tập xác định của hàm số.
  • Tính đạo hàm chính xác.
  • Lập bảng xét dấu đạo hàm một cách cẩn thận.
  • Phân biệt rõ các loại cực trị (cực đại, cực tiểu).

Tusach.vn - Đồng hành cùng bạn học Toán 12

Tusach.vn luôn đồng hành cùng các bạn học sinh trong quá trình học tập môn Toán 12. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các bài tập luyện tập để giúp các bạn đạt kết quả tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Ngoài ra, các bạn có thể tham khảo thêm các bài giải khác trong Chuyên đề học tập Toán 12 - Kết nối tri thức trên website của chúng tôi.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN