Giải mục 1 trang 6, 7, 8, 9 Chuyên đề học tập Toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 6, 7, 8, 9 Chuyên đề học tập Toán 12 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 6, 7, 8, 9 của Chuyên đề học tập Toán 12 - Kết nối tri thức. Bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức và rèn luyện kỹ năng giải bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đảm bảo cung cấp cho bạn nguồn tài liệu học tập đáng tin cậy.
Gieo một con xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi (X)là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó a) Các giá trị có thể của (X) là gì? b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được (X) sẽ nhận giá trị nào không?
Hoạt động 1
Trả lời câu hỏi Hoạt động 1 trang 6 Chuyên đề học tập Toán 12 Kết nối tri thức
Gieo một con xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi \(X\)là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó
a) Các giá trị có thể của \(X\) là gì?
b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được \(X\) sẽ nhận giá trị nào không?
Phương pháp giải:
Dựa vào thực nghiệm gieo một con xúc xắc 6 lần
Lời giải chi tiết:
a) \(X \in \left\{ {0;1;2;3;4;5;6} \right\}\).
b) Ta không thể khẳng định trước được.
Luyện tập 1
Trả lời câu hỏi Luyện tập 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên đồng thời 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X.
Phương pháp giải:
Bước 1: Liệt kê các giá trị có thể của X
Bước 2: Tính các xác suất để X nhận các giá trị đó
Bước 3: Lập bảng phân bố xác suất cho biến ngẫu nhiên X
Lời giải chi tiết:
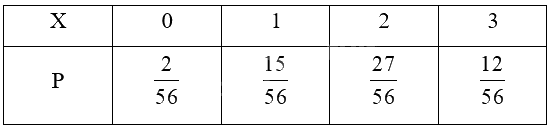
Các giá trị của X có thể nhận được thuộc tập {0; 1; 2; 3}.
Số kết quả có thể là \(C_{16}^3 = 560.\)
+ Biến cố \(\left\{ {X = 0} \right\}\) là: “Không có HS nam nào trong 3 HS được chọn”
Số cách chọn 3 học sinh nữ: \(C_6^3 = 20\) (cách chọn)
Do đó, \(P\left( {X = 0} \right)\; = \frac{{20}}{{560}} = \frac{2}{{56}}\)
+ Biến cố \(\left\{ {X = 1} \right\}\) là: “Chọn được 1 học sinh nam và 2 học sinh nữ”
Số cách chọn 1 học sinh nam và 2 học sinh nữ: \(C_{10}^1.C_6^2 = 150\) (cách chọn)
Do đó, \(P\left( {X = 1} \right)\; = \frac{{150}}{{560}} = \frac{{15}}{{56}}\)
+ Biến cố \(\left\{ {X = 2} \right\}\) là: “Chọn được 2 học sinh nam và 1 học sinh nữ”
Số cách chọn 2 học sinh nam và 1 học sinh nữ: \(C_{10}^2.C_6^1 = 270\) (cách chọn)
Do đó, \(P\left( {X = 2} \right)\; = \frac{{270}}{{560}} = \frac{{27}}{{56}}\)
+ Biến cố \(\left\{ {X = 3} \right\}\) là : “Chọn được 3 học sinh nam”
Số cách chọn 3 học sinh nam: \(C_{10}^3 = 120\) (cách chọn)
Do đó, \(P\left( {X = 3} \right)\; = \frac{{120}}{{560}} = \frac{{12}}{{56}}\)
Ta có bảng phân phối xác suất của X là:
Vận dụng 1
Trả lời câu hỏi Vận dụng 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một trò chơi sử dụng một hộp đựng 20 quả cầu có kích thước và khối lượng như nhau được ghi số từ 1 đến 20. Người chơi lấy ngẫu nhiên đồng thời 3 quả cầu trong hộp. Gọi X là số lớn nhất ghi trên 3 quả cầu đã lấy ra.
a) Lập bảng phân bố xác suất của X.
b) Người chơi thắng cuộc nếu trong 3 quả cầu lấy ra có ít nhất 1 quả cầu ghi số lớn hơn 18. Tính xác suất thắng của người chơi.
Phương pháp giải:
Làm theo hướng dẫn trong sách
Lời giải chi tiết:
a) Tập các giá trị có thể của X là {3; 4;...; 20}
Số kết quả có thể là \(C_{20}^3 = 1140.\)
Biến cố \(\left\{ {X = k} \right\}\) là biến cố: “Trong 3 quả cầu lấy ra có 1 quả cầu đánh số \(k\) và 2 quả cầu đánh số nhỏ hơn \(k\)”. Số kết quả thuận lợi là: \(C_{k - 1}^2\)
Vậy \(P\left( {X = k} \right) = \frac{{C_{k - 1}^2}}{{C_{20}^3}} = \frac{{(k - 1)(k - 2)}}{{2280}}\)
Bảng phân bố xác suất của X là:

b) Biến cố: “Người chơi thắng” là biến cố hợp của hai biến cố \(A = \left\{ {X = 19} \right\}\) và \(B = \left\{ {X = 20} \right\}\)
Vì \(A,B\) là hai biến cố xung khắc nên
\(P(A \cup B) = P(A) + P(B){\rm{ = }}P(X = 19) + P(X = 20) = 0,134 + 0,15 = 0,284\)
Hoạt động 2
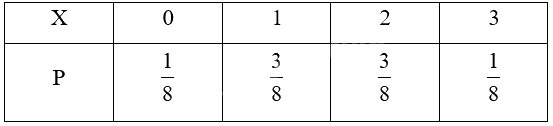
Trả lời câu hỏi Hoạt động 2 trang 7 Chuyên đề học tập Toán 12 Kết nối tri thức
Hãy nêu số thích hợp với dấu “?” để hoàn thành bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) trong Ví dụ 1.

Phương pháp giải:
Dựa vào HĐ1, ta điền các kết quả tương ứng vào bảng
Lời giải chi tiết:
- Hoạt động 1
- Hoạt động 2
- Luyện tập 1
- Vận dụng 1
Trả lời câu hỏi Hoạt động 1 trang 6 Chuyên đề học tập Toán 12 Kết nối tri thức
Gieo một con xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi \(X\)là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó
a) Các giá trị có thể của \(X\) là gì?
b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được \(X\) sẽ nhận giá trị nào không?
Phương pháp giải:
Dựa vào thực nghiệm gieo một con xúc xắc 6 lần
Lời giải chi tiết:
a) \(X \in \left\{ {0;1;2;3;4;5;6} \right\}\).
b) Ta không thể khẳng định trước được.
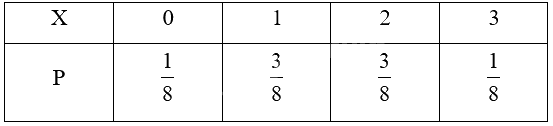
Trả lời câu hỏi Hoạt động 2 trang 7 Chuyên đề học tập Toán 12 Kết nối tri thức
Hãy nêu số thích hợp với dấu “?” để hoàn thành bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) trong Ví dụ 1.

Phương pháp giải:
Dựa vào HĐ1, ta điền các kết quả tương ứng vào bảng
Lời giải chi tiết:
Trả lời câu hỏi Luyện tập 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên đồng thời 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X.
Phương pháp giải:
Bước 1: Liệt kê các giá trị có thể của X
Bước 2: Tính các xác suất để X nhận các giá trị đó
Bước 3: Lập bảng phân bố xác suất cho biến ngẫu nhiên X
Lời giải chi tiết:
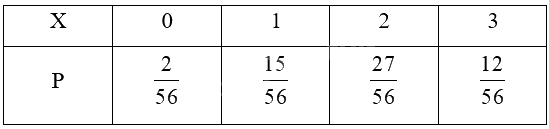
Các giá trị của X có thể nhận được thuộc tập {0; 1; 2; 3}.
Số kết quả có thể là \(C_{16}^3 = 560.\)
+ Biến cố \(\left\{ {X = 0} \right\}\) là: “Không có HS nam nào trong 3 HS được chọn”
Số cách chọn 3 học sinh nữ: \(C_6^3 = 20\) (cách chọn)
Do đó, \(P\left( {X = 0} \right)\; = \frac{{20}}{{560}} = \frac{2}{{56}}\)
+ Biến cố \(\left\{ {X = 1} \right\}\) là: “Chọn được 1 học sinh nam và 2 học sinh nữ”
Số cách chọn 1 học sinh nam và 2 học sinh nữ: \(C_{10}^1.C_6^2 = 150\) (cách chọn)
Do đó, \(P\left( {X = 1} \right)\; = \frac{{150}}{{560}} = \frac{{15}}{{56}}\)
+ Biến cố \(\left\{ {X = 2} \right\}\) là: “Chọn được 2 học sinh nam và 1 học sinh nữ”
Số cách chọn 2 học sinh nam và 1 học sinh nữ: \(C_{10}^2.C_6^1 = 270\) (cách chọn)
Do đó, \(P\left( {X = 2} \right)\; = \frac{{270}}{{560}} = \frac{{27}}{{56}}\)
+ Biến cố \(\left\{ {X = 3} \right\}\) là : “Chọn được 3 học sinh nam”
Số cách chọn 3 học sinh nam: \(C_{10}^3 = 120\) (cách chọn)
Do đó, \(P\left( {X = 3} \right)\; = \frac{{120}}{{560}} = \frac{{12}}{{56}}\)
Ta có bảng phân phối xác suất của X là:
Trả lời câu hỏi Vận dụng 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một trò chơi sử dụng một hộp đựng 20 quả cầu có kích thước và khối lượng như nhau được ghi số từ 1 đến 20. Người chơi lấy ngẫu nhiên đồng thời 3 quả cầu trong hộp. Gọi X là số lớn nhất ghi trên 3 quả cầu đã lấy ra.
a) Lập bảng phân bố xác suất của X.
b) Người chơi thắng cuộc nếu trong 3 quả cầu lấy ra có ít nhất 1 quả cầu ghi số lớn hơn 18. Tính xác suất thắng của người chơi.
Phương pháp giải:
Làm theo hướng dẫn trong sách
Lời giải chi tiết:
a) Tập các giá trị có thể của X là {3; 4;...; 20}
Số kết quả có thể là \(C_{20}^3 = 1140.\)
Biến cố \(\left\{ {X = k} \right\}\) là biến cố: “Trong 3 quả cầu lấy ra có 1 quả cầu đánh số \(k\) và 2 quả cầu đánh số nhỏ hơn \(k\)”. Số kết quả thuận lợi là: \(C_{k - 1}^2\)
Vậy \(P\left( {X = k} \right) = \frac{{C_{k - 1}^2}}{{C_{20}^3}} = \frac{{(k - 1)(k - 2)}}{{2280}}\)
Bảng phân bố xác suất của X là:

b) Biến cố: “Người chơi thắng” là biến cố hợp của hai biến cố \(A = \left\{ {X = 19} \right\}\) và \(B = \left\{ {X = 20} \right\}\)
Vì \(A,B\) là hai biến cố xung khắc nên
\(P(A \cup B) = P(A) + P(B){\rm{ = }}P(X = 19) + P(X = 20) = 0,134 + 0,15 = 0,284\)
Giải mục 1 trang 6, 7, 8, 9 Chuyên đề học tập Toán 12 - Kết nối tri thức: Tổng quan và hướng dẫn chi tiết
Mục 1 của Chuyên đề học tập Toán 12 - Kết nối tri thức thường tập trung vào việc giới thiệu các khái niệm cơ bản, định nghĩa, và tính chất quan trọng của một chủ đề mới. Việc nắm vững kiến thức nền tảng này là vô cùng quan trọng để giải quyết các bài tập phức tạp hơn trong tương lai. Tusach.vn sẽ cung cấp cho bạn lời giải chi tiết cho từng bài tập trong mục này, kèm theo các lưu ý quan trọng và phương pháp giải hiệu quả.
Nội dung chính của Mục 1 (trang 6, 7, 8, 9)
Để hiểu rõ hơn về Mục 1, chúng ta cần xác định chính xác nội dung mà nó bao gồm. Thông thường, Mục 1 sẽ giới thiệu:
- Các khái niệm mới: Định nghĩa, phân loại, ví dụ minh họa.
- Các tính chất quan trọng: Các định lý, quy tắc, công thức.
- Các ứng dụng cơ bản: Cách áp dụng kiến thức vào giải quyết các bài toán thực tế.
Giải chi tiết các bài tập trang 6, 7, 8, 9
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1, trang 6, 7, 8, 9 của Chuyên đề học tập Toán 12 - Kết nối tri thức:
Bài 1 (Trang 6)
(Nội dung bài tập và lời giải chi tiết)
Bài 2 (Trang 7)
(Nội dung bài tập và lời giải chi tiết)
Bài 3 (Trang 8)
(Nội dung bài tập và lời giải chi tiết)
Bài 4 (Trang 9)
(Nội dung bài tập và lời giải chi tiết)
Mẹo giải bài tập hiệu quả
Để giải các bài tập Toán 12 hiệu quả, bạn nên:
- Đọc kỹ đề bài và xác định yêu cầu của bài toán.
- Phân tích các dữ kiện đã cho và tìm mối liên hệ giữa chúng.
- Sử dụng các công thức, định lý, và tính chất đã học để giải bài toán.
- Kiểm tra lại kết quả và đảm bảo tính chính xác.
Ví dụ minh họa
Để giúp bạn hiểu rõ hơn về cách giải bài tập, chúng ta hãy xem xét một ví dụ minh họa:
(Ví dụ minh họa và lời giải chi tiết)
Lưu ý quan trọng
Khi học Toán 12, bạn cần lưu ý:
- Nắm vững các khái niệm cơ bản và định nghĩa.
- Hiểu rõ các tính chất quan trọng và cách áp dụng chúng.
- Luyện tập thường xuyên để rèn luyện kỹ năng giải bài tập.
- Tham khảo các nguồn tài liệu học tập khác nhau để mở rộng kiến thức.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn cam kết cung cấp cho bạn những lời giải bài tập Toán 12 chính xác, dễ hiểu và nhanh chóng. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác. Chúc bạn học tập tốt!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 6 | Dễ |
| Bài 2 | 7 | Trung bình |
| Bài 3 | 8 | Khó |
| Bài 4 | 9 | Trung bình |