Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề 2. Ứng dụng toán học để giải quyết một số bài toán tối ưu
Bài 4. Vận dụng đạo hàm để giải quyết một số bài toán tối ưu

Giải bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức

Giải bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức

Bài 2.9 trang 43 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích (5{rm{ }}l). Giá sản xuất mặt xung quanh là 100 nghìn đồng/m2, giá sản xuất mặt đáy là 120 nghìn đồng/m2. Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn? (Giả sử chi phí cho các mối nối không đáng kể)

Đề bài

Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích \(5{\rm{ }}l\). Giá sản xuất mặt xung quanh là 100 nghìn đồng/m2, giá sản xuất mặt đáy là 120 nghìn đồng/m2. Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn (giả sử chi phí cho các mối nối không đáng kể)?

Phương pháp giải - Xem chi tiếtGiải bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức 1

Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.

Lời giải chi tiết

Đổi: 5 lít = 5 \(d{m^3}\) = 0,005 \({m^3}\).

Gọi r (m) là bán kính của đáy thùng đựng sơn hình trụ, r > 0.

h (m) là chiều cao thùng sơn hình trụ, h > 0.

Ta có \({V_{tru}} = \pi {r^2}h \Leftrightarrow 0,005 = \pi {r^2}h \Leftrightarrow h = \frac{{0,005}}{{\pi {r^2}}}\) (m).

Diện tích xung quanh thùng sơn là: \({S_{xq}} = 2\pi rh = 2\pi r.\frac{{0,005}}{{\pi {r^2}}} = \frac{{0,01}}{r}\) \(\left( {{m^2}} \right)\).

Diện tích đáy thùng sơn là: \({S_{day}} = \pi {r^2}\) \(\left( {{m^2}} \right)\).

Giá sản xuất mặt xung quanh của một thùng sơn là:

\(100{S_{xq}} = 100.\frac{{0,01}}{r} = \frac{1}{r}\) (nghìn đồng).

Giá sản xuất mặt hai mặt đáy của một thùng sơn là:

\(120.2.\pi {r^2} = 240\pi {r^2}\) (nghìn đồng).

Chi phí sản xuất một thùng sơn là:

\(C(r) = \frac{1}{r} + 240\pi {r^2}\) (nghìn đồng).

Xét \(C'(r) = - \frac{1}{{{r^2}}} + 480\pi r = 0 \Leftrightarrow 480\pi r = \frac{1}{{{r^2}}} \Leftrightarrow 480\pi {r^3} = 1 \Leftrightarrow r = \sqrt[3]{{\frac{1}{{480\pi }}}}\).

Bảng biến thiên của hàm số C(r) trên \(\left( {0; + \infty } \right)\):

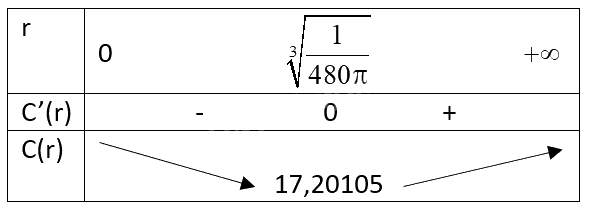
Giải bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức 2

Từ bảng biến thiên, ta thấy giá trị nhỏ nhất của C(r) là xấp xỉ 17,20105 nghìn đồng.

Ta có \(\frac{{1000000}}{{17,20105}} \approx 58135,98533\).

Vậy công ty có thể sản xuất được tối đa 58135 thùng sơn.

Giải bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức: Hướng dẫn chi tiết

Bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh khảo sát hàm số và tìm các điểm cực trị. Để giải bài này, chúng ta cần nắm vững các bước sau:

  1. Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
  2. Tính đạo hàm bậc nhất: Tính f'(x) để tìm các điểm dừng (điểm mà f'(x) = 0 hoặc không xác định).
  3. Lập bảng biến thiên: Xác định dấu của f'(x) trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến.
  4. Tìm cực trị: Sử dụng dấu của f'(x) để xác định các điểm cực đại, cực tiểu.
  5. Khảo sát giới hạn: Tính giới hạn của hàm số khi x tiến tới vô cùng và các điểm gián đoạn.
  6. Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập để vẽ đồ thị hàm số.

Lời giải chi tiết bài 2.9 trang 43

Để minh họa, giả sử hàm số cần khảo sát là: f(x) = x3 - 3x2 + 2

Bước 1: Tập xác định

Hàm số f(x) = x3 - 3x2 + 2 xác định trên tập số thực R.

Bước 2: Đạo hàm bậc nhất

f'(x) = 3x2 - 6x

Bước 3: Tìm điểm dừng

Giải phương trình f'(x) = 0:

3x2 - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2 là các điểm dừng.

Bước 4: Lập bảng biến thiên

x-∞02+∞
f'(x)+-+
f(x)Đồng biếnNghịch biếnĐồng biến

Bước 5: Tìm cực trị

Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên x = 0 là điểm cực đại. Giá trị cực đại là f(0) = 2.

Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên x = 2 là điểm cực tiểu. Giá trị cực tiểu là f(2) = -2.

Bước 6: Khảo sát giới hạn

limx→-∞ f(x) = -∞

limx→+∞ f(x) = +∞

Lưu ý khi giải bài tập khảo sát hàm số

  • Nắm vững các khái niệm về đạo hàm, cực trị, khoảng đồng biến, nghịch biến.
  • Thực hành giải nhiều bài tập để làm quen với các dạng bài khác nhau.
  • Sử dụng máy tính cầm tay để kiểm tra lại kết quả.

Tusach.vn hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức và đạt kết quả tốt trong môn Toán.

Ngoài ra, các em có thể tham khảo thêm các bài giải khác tại tusach.vn.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN