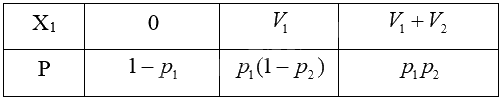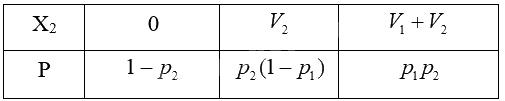Đề bài
Một cuộc thi gồm hai loại câu hỏi. Câu hỏi loại 1 và câu hỏi loại 2. Ở vòng 1 thí sinh bốc ngẫu nhiên câu hỏi loại \(i \in \left\{ {1;{\rm{ }}2} \right\}\). Nếu trả lời sai thì thí sinh dừng cuộc thi tại đây. Nếu trả lời đúng, thí sinh sẽ đi tiếp vào vòng 2, tiếp tục bốc ngẫu nhiên một câu hỏi loại \(j \in \left\{ {1;{\rm{ }}2} \right\}(j \ne i).\) Sau khi thí sinh trả lời câu hỏi này, cuộc thi kết thúc. Thí sinh sẽ nhận được \({V_i}\) điểm nếu trả lời đúng câu hỏi loại \(i \in \left\{ {1;{\rm{ }}2} \right\}\). Giả thiết rằng việc trả lời đúng câu hỏi vòng 1 sẽ không ảnh hưởng đến xác suất trả lời đúng hay sai câu hỏi ở vòng 2. Bạn An tham gia cuộc thi. Gọi \({E_i}\) là biển cố: "An trả lời đúng câu hỏi loại \(i\)”(\(i \in \left\{ {1;{\rm{ }}2} \right\}\)). Giả sử \(P(E) = {p_i}\).
a) Với điều kiện nào thì ở vòng 1, An nên bốc ngẫu nhiên câu hỏi loại 1?
b) Giả sử \({p_1} = 0,6;{p_2} = 0,8;{V_1} = 20;{V_2} = 10\). Khi đó ở vòng 1, An nên bắc ngẫu nhiên câu hỏi loại nào?
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của biến ngẫu nhiên rời rạc, công thức nhân xác suất của 2 biến cố độc lập.
Lời giải chi tiết
Trường hợp 1: Nếu ở vòng 1 An bốc ngẫu nhiên câu hỏi loại 1.
+ Nếu trả lời sai thì An được 0 điểm. Cuộc thi kết thúc tại đây.
Vậy \(P({X_1} = 0) = P(\overline {{E_1}} ) = 1 - {p_1}.\)
+ Nếu trả lời đúng thì An nhận \({V_1}\) điểm và An được đi tiếp vòng 2: Bốc ngẫu nhiên một câu hỏi loại 2.
\({E_i}\) là biến cố: “Trả lời đúng câu hỏi loại \(i\)”, \(i \in \left\{ {1;2} \right\}\).
Nếu trả lời sai câu hỏi loại 2 thì An nhận 0 điểm. Cuộc thi kết thúc và An nhận được \({V_1}\) điểm.
Theo giả thiết \({E_1},\overline {{E_2}} \) là hai biến cố độc lập. Theo công thức nhân xác suất ta có:
\(P({X_1} = {V_1}) = P({E_1}\overline {{E_2}} ) = P({E_1}).P(\overline {{E_2}} ) = {p_1}(1 - {p_2})\)
Nếu trả lời đúng câu hỏi loại 2 thì An nhận \({V_2}\) điểm. Cuộc thi kết thúc và An nhận được \({V_1} + {V_2}\) điểm.
Theo giả thiết \({E_1},{E_2}\) là hai biến cố độc lập. Theo công thức nhân xác suất ta có:
\(P({X_1} = {V_1} + {V_2}) = P({E_1}{E_2}) = P({E_1}).P({E_2}) = {p_1}{p_2}\)
Ta có bảng phân bố xác suất của \({X_1}\) là:
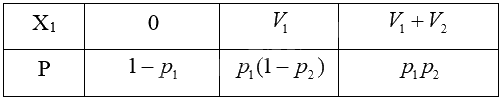
\(E({X_1}) = {V_1}{p_1}(1 - {p_2}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2}\)
Trường hợp 2: Nếu ở vòng 1 An bốc ngẫu nhiên câu hỏi loại 2.
Tương tự trường hợp 1, ta có bảng phân bố xác suất của \({X_2}\) là:
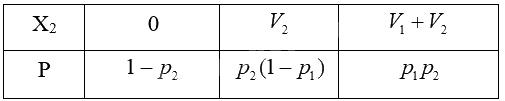
\(E({X_2}) = {V_2}{p_2}(1 - {p_1}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2}\)
a) Ở vòng 1 An nên chọn câu hỏi loại 1 trước nếu:
\(\begin{array}{l}E({X_1}) \ge E({X_2}) \Leftrightarrow {V_1}{p_1}(1 - {p_2}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2} > {V_2}{p_2}(1 - {p_1}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2}\\{\rm{ }} \Leftrightarrow {V_1}{p_1}(1 - {p_2}) \ge {V_2}{p_2}(1 - {p_1})\\{\rm{ }} \Leftrightarrow \frac{{{V_1}{p_1}}}{{1 - {p_1}}} \ge \frac{{{V_2}{p_2}}}{{1 - {p_2}}}\end{array}\)
b) Ta có: \(\frac{{{V_1}{p_1}}}{{1 - {p_1}}} = \frac{{20.0,6}}{{1 - 0,6}} = 30;\frac{{{V_2}{p_2}}}{{1 - {p_2}}} = \frac{{10.0,8}}{{1 - 0,8}} = 40\)
Ta thấy \(\frac{{{V_1}{p_1}}}{{1 - {p_1}}} < \frac{{{V_2}{p_2}}}{{1 - {p_2}}}\)nên ở vòng 1 An nên chọn câu hỏi loại 2 trước.