Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề 2. Ứng dụng toán học để giải quyết một số bài toán tối ưu
Bài tập cuối chuyên đề 2

Giải bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức

Giải bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 2.12 trang 44 Chuyên đề học tập Toán 12 Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.

Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập Toán 12, giúp các em tự tin hơn trong quá trình học tập.

Một nhà máy sản xuất hai loại sản phẩm, mỗi sản phẩm yêu cầu sử dụng ba máy. Máy đầu tiên có thể được sử dụng nhiều nhất là 70 giờ, máy thứ hai nhiều nhất là 40 giờ và máy thứ ba nhiều nhất là 90 giờ. Sản phẩm thứ nhất cần 2 giờ trên máy 1, 1 giờ trên máy II và 1 giờ trên máy III; sản phẩm thứ hai cần 1 giờ cho mỗi máy I, II và 3 giờ trên máy III. Nếu lợi nhuận là 400 nghìn đồng/đơn vị cho sản phẩm thứ nhất và 600 nghìn đồng/đơn vị cho sản phẩm thứ hai, thì cần sản xuất bao nhiều đơn vị mỗi sản

Đề bài

Một nhà máy sản xuất hai loại sản phẩm, mỗi sản phẩm yêu cầu sử dụng ba máy. Máy đầu tiên có thể được sử dụng nhiều nhất là 70 giờ, máy thứ hai nhiều nhất là 40 giờ và máy thứ ba nhiều nhất là 90 giờ. Sản phẩm thứ nhất cần 2 giờ trên máy 1, 1 giờ trên máy II và 1 giờ trên máy III; sản phẩm thứ hai cần 1 giờ cho mỗi máy I, II và 3 giờ trên máy III. Nếu lợi nhuận là 400 nghìn đồng/đơn vị cho sản phẩm thứ nhất và 600 nghìn đồng/đơn vị cho sản phẩm thứ hai, thì cần sản xuất bao nhiều đơn vị mỗi sản phẩm để lợi nhuận thu được là lớn nhất?

Phương pháp giải - Xem chi tiếtGiải bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức 1

F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác. Tính giá trị của F(x; y) tại các điểm cực biên.

Lời giải chi tiết

Gọi x và y lần lượt là số sản phẩm thứ nhất và sản phẩm thứ hai cần sản xuất.

Lợi nhuận thu được là: 400x + 600y (nghìn đồng).

Ta có hệ bất phương trình sau:

\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\2x + y \le 70\\x + y \le 40\\x + 3y \le 90\end{array} \right.\)

Miền nghiệm của hệ bất phương trình này là miền ngũ giác OABCD được tô màu như hình vẽ dưới đây:

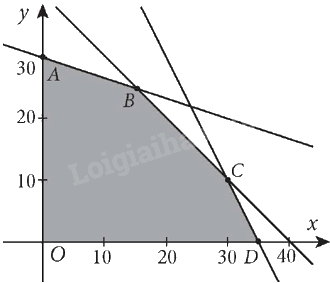
Giải bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức 2

Các điểm cực biên là: O(0; 0), A(0; 30), B(15; 25), C(30; 10), D(35; 0).

Ta có: \(F(0;0) = 0,F(0,30) = 18000;F(15;25) = 21000;F(30;10) = 18000;F(35;0) = 14000\)

Vậy lợi nhuận thu được lớn nhất là 21 000 nghìn đồng khi x = 15 và y = 25, tức là cần sản xuất 15 sản phẩm thứ nhất và 25 sản phẩm thứ hai.

Giải bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức: Tổng quan

Bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung bài tập 2.12 trang 44

Bài tập 2.12 thường có dạng như sau: Cho một hàm số y = f(x). Yêu cầu học sinh:

  • Tính đạo hàm f'(x).
  • Tìm các điểm cực trị của hàm số.
  • Xác định khoảng đồng biến, nghịch biến của hàm số.
  • Vẽ đồ thị hàm số.

Lời giải chi tiết bài 2.12 trang 44

Để giải bài tập 2.12 trang 44, chúng ta cần thực hiện các bước sau:

  1. Bước 1: Tính đạo hàm f'(x). Sử dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của hàm số y = f(x).
  2. Bước 2: Tìm các điểm cực trị. Giải phương trình f'(x) = 0 để tìm các điểm nghiệm. Sau đó, xét dấu của f'(x) trên các khoảng xác định để xác định các điểm cực đại, cực tiểu.
  3. Bước 3: Xác định khoảng đồng biến, nghịch biến. Dựa vào dấu của f'(x) trên các khoảng xác định, ta có thể xác định khoảng đồng biến (f'(x) > 0) và khoảng nghịch biến (f'(x) < 0) của hàm số.
  4. Bước 4: Vẽ đồ thị hàm số. Sử dụng các thông tin đã tìm được ở các bước trên để vẽ đồ thị hàm số y = f(x).

Ví dụ minh họa

Bài toán: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị và khoảng đồng biến, nghịch biến của hàm số.

Lời giải:

  1. Tính đạo hàm: y' = 3x2 - 6x
  2. Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
  3. Xác định khoảng đồng biến, nghịch biến:
    • Với x < 0, y' > 0 nên hàm số đồng biến trên (-∞, 0).
    • Với 0 < x < 2, y' < 0 nên hàm số nghịch biến trên (0, 2).
    • Với x > 2, y' > 0 nên hàm số đồng biến trên (2, +∞).

Mẹo giải bài tập

  • Nắm vững các quy tắc tính đạo hàm.
  • Sử dụng bảng xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến và cực trị.
  • Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.

Tài liệu tham khảo

Để hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm, các em có thể tham khảo:

  • Sách giáo khoa Toán 12 - Kết nối tri thức
  • Các bài giảng trực tuyến về đạo hàm
  • Các bài tập luyện tập về đạo hàm

Kết luận

Bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn trong quá trình học tập.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN