Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề học tập Toán 12 - Kết nối tri thức
Chuyên đề 2. Ứng dụng toán học để giải quyết một số bài toán tối ưu
Bài 3. Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính

Giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức

Giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức

Bài 2.4 trang 33 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hãy cùng Tusach.vn khám phá lời giải chi tiết bài 2.4 trang 33 ngay dưới đây!

Chế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F1 và F2 mỗi đơn vị F1 giá 1 200 đồng và mỗi đơn vị F2 giá 720 đồng. Mỗi đơn vị thức ăn F1 chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F2 chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế độ hỗn hợp F1 và F2 sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng.

Đề bài

Chế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F1 và F2 mỗi đơn vị F1 giá 1 200 đồng và mỗi đơn vị F2 giá 720 đồng. Mỗi đơn vị thức ăn F1 chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F2 chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế độ hỗn hợp F1 và F2 sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng.

Phương pháp giải - Xem chi tiếtGiải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức 1

Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.

Lời giải chi tiết

Gọi x và y lần lượt là chế ăn hỗn hợp F1 và F2.

Chi phí cho thức ăn là: 1 200x + 720y (đồng).

Ta có hệ bất phương trình sau:

\(\left\{ \begin{array}{l}x \ge 0;y \ge 0\\2{\rm{x}} + y \ge 400\\x + 2y \ge 500\\4{\rm{x}} + 4y \ge 1{\rm{ }}400\end{array} \right.\)

Miền nghiệm của hệ bất phương trình này là miền tô màu, không bị chặn như hình vẽ dưới đây:

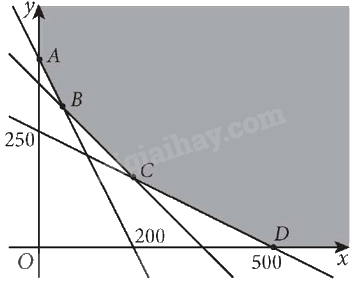
Giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức 2

Các điểm cực biên là: A(0; 400), B(50; 300), C(200; 150), D(500; 0).

Ta có:

F(0; 400) = 1 200.0 + 720.400 = 288 000;

F(50; 300) = 1 200.50 + 720.300 = 276 000;

F(200; 150) = 1 200.200 + 720.150 = 348 000;

F(500; 0) = 1 200.500 + 720.0 = 600 000.

Do đó giá trị nhỏ nhất của F(x; y) bằng 276 000 tại điểm cực biên B(50; 300).

Vậy để chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng thì cần 50 chế ăn loại F1 và 300 chế ăn loại F2.

Giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức: Tổng quan và Phương pháp

Bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến sự biến thiên của hàm số. Cụ thể, bài toán thường tập trung vào việc tìm khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các bước sau:

  1. Xác định tập xác định của hàm số: Đây là bước đầu tiên và quan trọng để đảm bảo tính chính xác của các bước tiếp theo.
  2. Tính đạo hàm cấp nhất (y'): Đạo hàm cấp nhất đóng vai trò quan trọng trong việc xác định khoảng đồng biến, nghịch biến và cực trị của hàm số.
  3. Tìm các điểm tới hạn: Các điểm tới hạn là các điểm mà đạo hàm cấp nhất bằng 0 hoặc không xác định.
  4. Khảo sát dấu của đạo hàm cấp nhất: Dựa vào dấu của đạo hàm cấp nhất trên các khoảng xác định, ta có thể xác định khoảng đồng biến, nghịch biến của hàm số.
  5. Tìm cực trị của hàm số: Sử dụng đạo hàm cấp hai (y'') hoặc xét dấu của đạo hàm cấp nhất để xác định cực đại, cực tiểu của hàm số.
  6. Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập được, ta có thể vẽ đồ thị hàm số một cách chính xác.

Lời giải chi tiết bài 2.4 trang 33

Để minh họa phương pháp trên, chúng ta sẽ cùng giải chi tiết bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức. (Giả sử bài toán cụ thể là: Khảo sát hàm số y = x3 - 3x2 + 2)

Bước 1: Xác định tập xác định

Hàm số y = x3 - 3x2 + 2 có tập xác định là D = ℝ.

Bước 2: Tính đạo hàm cấp nhất

y' = 3x2 - 6x

Bước 3: Tìm các điểm tới hạn

y' = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2

Bước 4: Khảo sát dấu của đạo hàm cấp nhất

x-∞02+∞
y'+-+
yNBĐBNB

(NB: Đồng biến, ĐB: Nghịch biến)

Bước 5: Tìm cực trị của hàm số

y'' = 6x - 6

y''(0) = -6 < 0 ⇒ Hàm số đạt cực đại tại x = 0, yCĐ = 2

y''(2) = 6 > 0 ⇒ Hàm số đạt cực tiểu tại x = 2, yCT = -2

Bước 6: Vẽ đồ thị hàm số

(Phần này cần mô tả cách vẽ đồ thị dựa trên các thông tin đã tìm được. Có thể sử dụng các công cụ vẽ đồ thị trực tuyến để minh họa.)

Lưu ý khi giải bài tập

  • Luôn kiểm tra lại các bước tính toán để tránh sai sót.
  • Hiểu rõ ý nghĩa của đạo hàm và ứng dụng của nó trong việc khảo sát hàm số.
  • Luyện tập thường xuyên để nắm vững phương pháp giải bài tập.

Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học

Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập Toán 12 Kết nối tri thức. Hãy truy cập Tusach.vn để học tập và ôn luyện hiệu quả!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN