Giải mục 5 trang 17, 18, 19, 20 Chuyên đề học tập Toán 11 - Cánh diều
Tổng quan nội dung
Giải mục 5 trang 17, 18, 19, 20 Chuyên đề học tập Toán 11 - Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 5 trang 17, 18, 19, 20 của Chuyên đề học tập Toán 11, sách Cánh Diều. Bài giải này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và giúp học sinh hiểu sâu sắc kiến thức.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập tốt nhất để hỗ trợ các em học sinh trong quá trình học tập.
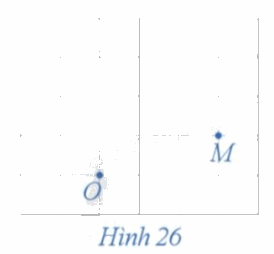
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Luyện tập 8
Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
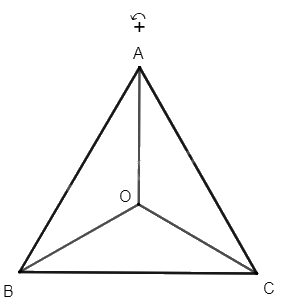
Ta có tam giác ABC đều có O là trọng tâm nên \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 120^\circ \) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC\). Vì phép quay với góc quay – 120° có chiều quay cùng chiều kim đồng hồ nên ảnh của các điểm A, B, C qua phép quay tâm O với góc quay – 120° lần lượt là các điểm C, A, B.
Luyện tập 9
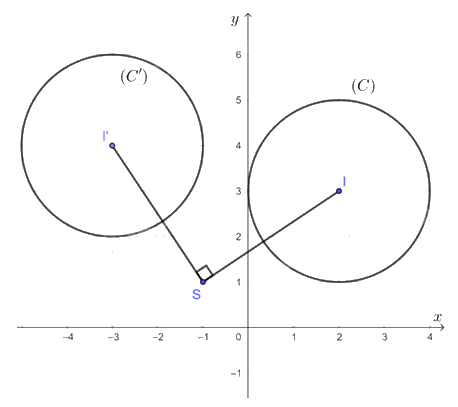
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°.
Phương pháp giải:
Tìm ảnh của tâm I qua phép quay bằng cách:
Phép quay tâm O, góc 900: Khi đó: \(\left\{ \begin{array}{l}x' = - y\\y' = x\end{array} \right.\)
Từ đó xác định ảnh của (C)
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của I qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Suy ra I'(– 3; 4).
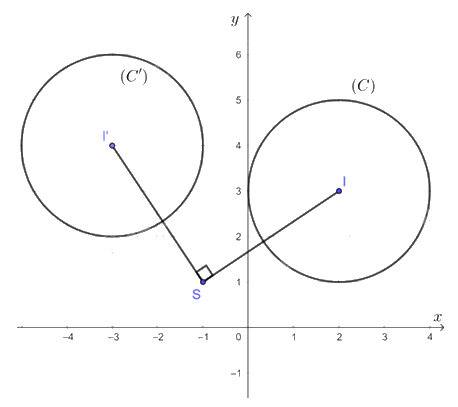
Vậy ảnh đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là đường tròn (C') có tâm I'(– 3; 4), bán kính R' = 2.
Hoạt động 13
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Phương pháp giải:
- Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob.
Kí hiệu: (Oa, Ob).
- Xác định điểm M' thỏa mãn điều kiện: OM' = OM và góc lượng giác (OM, OM') = 90°
Lời giải chi tiết:
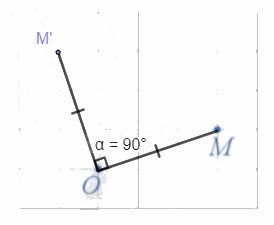
Cách xác định:
- Nối O với M;
- Qua O kẻ đường thẳng vuông góc với OM, trên đường thẳng, lấy điểm M' theo chiều dương sao cho OM' = OM.
Hoạt động 15
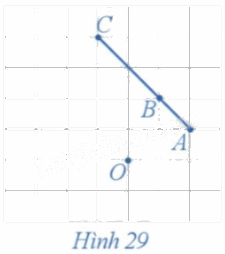
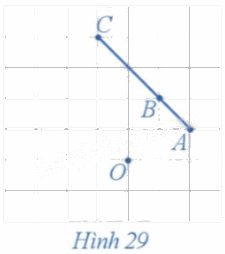
Xét phép quay tâm O với góc quay 90° (Hình 29).
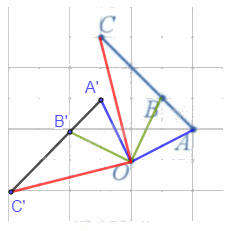
a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
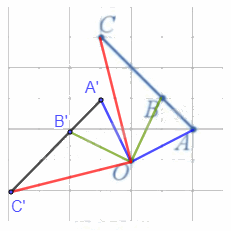
a) Các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay tâm O, góc quay 90° được xác định như hình vẽ trên.
b) Nhận thấy ba điểm A', B', C' thẳng hàng và B' nằm giữa A' và C'.
Hoạt động 14
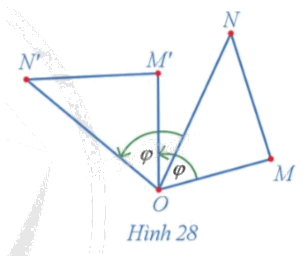
Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ.
a) Hai tam giác OM'N' và OMN có bằng nhau hay không?
b) So sánh hai đoạn thẳng M'N' và MN.
Phương pháp giải:
Xét 2 tam giác OM'N' và OMN bằng nhau theo trường hợp c – g – c. Từ đó so sánh hai đoạn thẳng M'N' và MN.
Lời giải chi tiết:
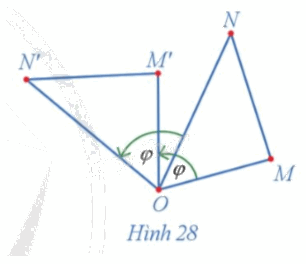
a) Vì M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay \(\varphi \) nên \(OM{\rm{ }} = {\rm{ }}OM',{\rm{ }}ON{\rm{ }} = {\rm{ }}ON'.\)
Ta có:
\(\begin{array}{l}\widehat {MON} + \widehat {NOM'} = \widehat {MOM'} = \varphi \\\widehat {NOM'} + \widehat {M'ON'} = \widehat {NON'} = \varphi \end{array}\)
Suy ra \(\widehat {MON} = \widehat {M'ON'}\)
Xét hai tam giác OM'N' và OMN ta có:
OM = OM' (cmt)
\(\widehat {MON} = \widehat {M'ON'}\) cmt)
ON = ON' (cmt)
Do đó, hai tam giác OM'N' và OMN bằng nhau (c – g – c).
b) Từ \(\Delta OM'N'{\rm{ }} = {\rm{ }}\Delta OMN\), suy ra M'N' = MN (hai cạnh tương ứng).
- Hoạt động 13
- Luyện tập 8
- Hoạt động 14
- Hoạt động 15
- Luyện tập 9
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Phương pháp giải:
- Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob.
Kí hiệu: (Oa, Ob).
- Xác định điểm M' thỏa mãn điều kiện: OM' = OM và góc lượng giác (OM, OM') = 90°
Lời giải chi tiết:
Cách xác định:
- Nối O với M;
- Qua O kẻ đường thẳng vuông góc với OM, trên đường thẳng, lấy điểm M' theo chiều dương sao cho OM' = OM.
Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
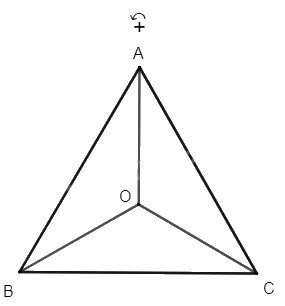
Ta có tam giác ABC đều có O là trọng tâm nên \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 120^\circ \) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC\). Vì phép quay với góc quay – 120° có chiều quay cùng chiều kim đồng hồ nên ảnh của các điểm A, B, C qua phép quay tâm O với góc quay – 120° lần lượt là các điểm C, A, B.
Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ.
a) Hai tam giác OM'N' và OMN có bằng nhau hay không?
b) So sánh hai đoạn thẳng M'N' và MN.
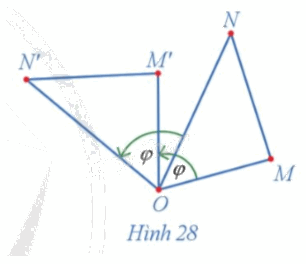
Phương pháp giải:
Xét 2 tam giác OM'N' và OMN bằng nhau theo trường hợp c – g – c. Từ đó so sánh hai đoạn thẳng M'N' và MN.
Lời giải chi tiết:
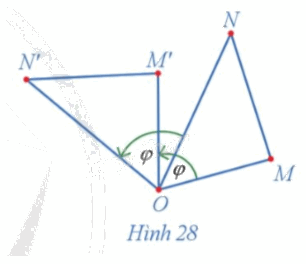
a) Vì M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay \(\varphi \) nên \(OM{\rm{ }} = {\rm{ }}OM',{\rm{ }}ON{\rm{ }} = {\rm{ }}ON'.\)
Ta có:
\(\begin{array}{l}\widehat {MON} + \widehat {NOM'} = \widehat {MOM'} = \varphi \\\widehat {NOM'} + \widehat {M'ON'} = \widehat {NON'} = \varphi \end{array}\)
Suy ra \(\widehat {MON} = \widehat {M'ON'}\)
Xét hai tam giác OM'N' và OMN ta có:
OM = OM' (cmt)
\(\widehat {MON} = \widehat {M'ON'}\) cmt)
ON = ON' (cmt)
Do đó, hai tam giác OM'N' và OMN bằng nhau (c – g – c).
b) Từ \(\Delta OM'N'{\rm{ }} = {\rm{ }}\Delta OMN\), suy ra M'N' = MN (hai cạnh tương ứng).
Xét phép quay tâm O với góc quay 90° (Hình 29).
a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
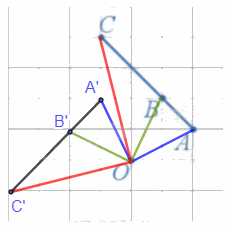
a) Các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay tâm O, góc quay 90° được xác định như hình vẽ trên.
b) Nhận thấy ba điểm A', B', C' thẳng hàng và B' nằm giữa A' và C'.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°.
Phương pháp giải:
Tìm ảnh của tâm I qua phép quay bằng cách:
Phép quay tâm O, góc 900: Khi đó: \(\left\{ \begin{array}{l}x' = - y\\y' = x\end{array} \right.\)
Từ đó xác định ảnh của (C)
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của I qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Suy ra I'(– 3; 4).
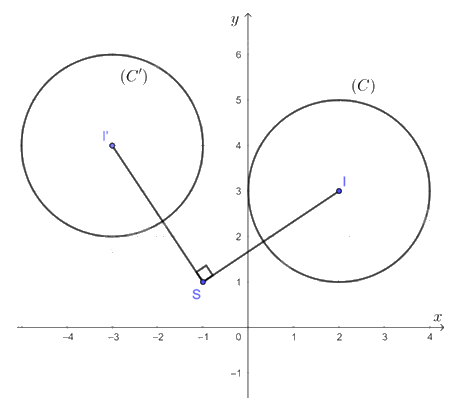
Vậy ảnh đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là đường tròn (C') có tâm I'(– 3; 4), bán kính R' = 2.
Giải mục 5 trang 17, 18, 19, 20 Chuyên đề học tập Toán 11 - Cánh Diều: Tổng quan và hướng dẫn chi tiết
Mục 5 trong Chuyên đề học tập Toán 11 Cánh Diều tập trung vào một phần kiến thức quan trọng, thường liên quan đến một chủ đề cụ thể trong chương trình. Việc nắm vững nội dung này là nền tảng để giải quyết các bài tập phức tạp hơn và đạt kết quả tốt trong các kỳ thi.
Nội dung chính của mục 5
Để hiểu rõ hơn về mục 5, chúng ta cần xác định các nội dung chính mà nó đề cập đến. Thông thường, mục này sẽ bao gồm:
- Định nghĩa và khái niệm: Các khái niệm cơ bản liên quan đến chủ đề được trình bày rõ ràng và dễ hiểu.
- Tính chất và định lý: Các tính chất và định lý quan trọng được chứng minh và giải thích chi tiết.
- Ví dụ minh họa: Các ví dụ minh họa giúp học sinh hiểu rõ cách áp dụng kiến thức vào thực tế.
- Bài tập áp dụng: Các bài tập áp dụng giúp học sinh rèn luyện kỹ năng và củng cố kiến thức.
Giải chi tiết các bài tập trang 17, 18, 19, 20
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 5, trang 17, 18, 19, 20 của Chuyên đề học tập Toán 11 Cánh Diều:
Bài 1: (Trang 17)
(Nội dung bài tập và lời giải chi tiết)
Bài 2: (Trang 18)
(Nội dung bài tập và lời giải chi tiết)
Bài 3: (Trang 19)
(Nội dung bài tập và lời giải chi tiết)
Bài 4: (Trang 20)
(Nội dung bài tập và lời giải chi tiết)
Mẹo giải bài tập hiệu quả
Để giải các bài tập trong mục 5 một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của đề bài trước khi bắt đầu giải.
- Xác định kiến thức cần sử dụng: Xác định các khái niệm, tính chất và định lý liên quan đến bài tập.
- Lập kế hoạch giải: Lập kế hoạch giải bài tập một cách logic và có hệ thống.
- Kiểm tra lại kết quả: Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tập hiệu quả hơn:
- Sách bài tập Toán 11 Cánh Diều
- Các trang web học tập trực tuyến
- Các video bài giảng trên YouTube
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về mục 5 trang 17, 18, 19, 20 Chuyên đề học tập Toán 11 Cánh Diều và đạt kết quả tốt trong học tập. Chúc các bạn học tốt!