Lựa chọn câu để xem lời giải nhanh hơn- Hoạt động 1
- Luyện tập 1
- Hoạt động 2
- Luyện tập 2
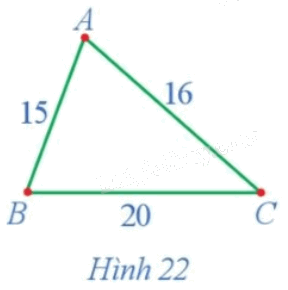
Giả sử ba địa điểm A, B, C được nối với nhau theo những con đường AB, BC, CA với độ dài lần lượt là 15 km, 20 km, 16 km. Sử dụng đồ thị để mô tả tình huống đó.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
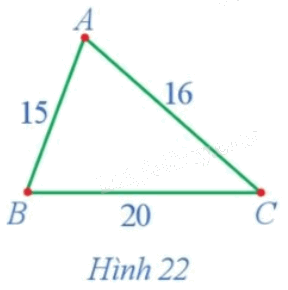
Đồ thị ở Hình 22 mô tả tình huống trong hoạt động này.
Hãy cho ví dụ về đồ thị có trọng số.
Phương pháp giải:
Nếu mỗi cạnh của đồ thị G được gắn với một số thực (có thể là độ dài của đường đi trên mỗi cạnh, chi phí vận chuyển trên mỗi cạnh đó,…) thì đồ thị G được gọi là đồ thị có trọng số.
Lời giải chi tiết:
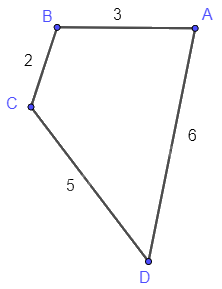
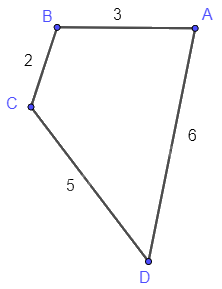
Ví dụ về đồ thị có trọng số: Có 4 trạm xe bus A, B, C, D được nối với nhau theo những con đường AB, BC, CD, DA với độ dài lần lượt là 3 km, 2 km, 5 km, 6 km. Ta có đồ thị mô tả tình huống trên như sau.
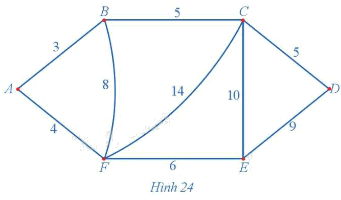
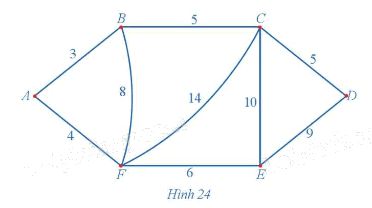
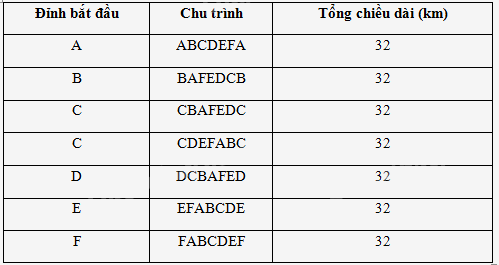
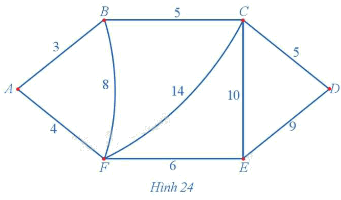
Giả sử có sáu địa điểm A, B, C, D, E, F được nối với nhau theo những con đường với độ dài (đơn vị: kilômét) được mô tả bằng đồ thị có trọng số ở Hình 24. Người giao hàng cần đi giao hàng tại sáu địa điểm trên. Người giao hàng xuất phát từ một địa điểm nào đó, đi qua các địa điểm còn lại để giao hàng và trở về địa điểm ban đầu. Hãy tìm một đường đi thỏa mãn điều kiện trên cho người giao hàng sao cho quãng đường mà người giao hàng phải di chuyển là ngắn nhất.
Phương pháp giải:
Tìm các con đường thỏa mãn điều kiện để bài, sau đó so sánh xem quãng đường nào ngắn nhất.
Lời giải chi tiết:
Để tìm quãng đường đi ngắn nhất trên đồ thị có trọng số, ta áp dụng thuật toán láng giềng gần nhất để tìm tất cả các chu trình xuất phát từ một đỉnh ban đầu, đi qua các đỉnh khác và trở về đỉnh ban đầu sao cho tổng độ dài các cạnh của chu trình đó là ngắn nhất. Sau đó, ta so sánh độ dài của tất cả các chu trình “tốt nhất” vừa tìm được để tìm ra chu trình có tổng độ dài các cạnh là ngắn nhất. Việc giải cụ thể Hoạt động 2 trang 46, ta cùng xem chi tiết ở Luyện tập 2 trang 46.
Sử dụng thuật toán láng giềng gần nhất để giải bài toán trong Hoạt động 2.
Phương pháp giải:
Để tìm quãng đường đi ngắn nhất trên đồ thị có trọng số, ta áp dụng thuật toán láng giềng gần nhất để tìm tất cả các chu trình xuất phát từ một đỉnh ban đầu, đi qua các đỉnh khác và trở về đỉnh ban đầu sao cho tổng độ dài các cạnh của chu trình đó là ngắn nhất. Sau đó, ta so sánh độ dài của tất cả các chu trình “tốt nhất” vừa tìm được để tìm ra chu trình có tổng độ dài các cạnh là ngắn nhất.
Lời giải chi tiết:
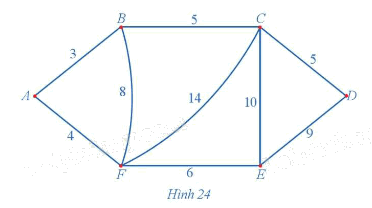
Dễ thấy đồ thị Hình 24 có chu trình Hamilton.
+) Sử dụng thuật toán láng giềng gần nhất đối với đỉnh xuất phát A, ta có:
Từ A, đỉnh gần nhất là B, AB = 3 km;
Từ B, đỉnh chưa đến gần nhất là C, BC = 5 km;
Từ C, đỉnh chưa đến gần nhất là D, CD = 5 km;
Từ D, đỉnh chưa đến gần nhất là E, DE = 9 km;
Từ E, đỉnh chưa đến gần nhất là F, EF = 6 km;
Đến đây không còn đỉnh chưa đến, vì vậy quay về A, FA = 4 km.
Tổng quãng đường theo chu trình ABCDEFA là: 3 + 5 + 5 + 9 + 6 + 4 = 32 (km).
Tương tự bắt đầu với những đỉnh khác, ta có bảng sau:
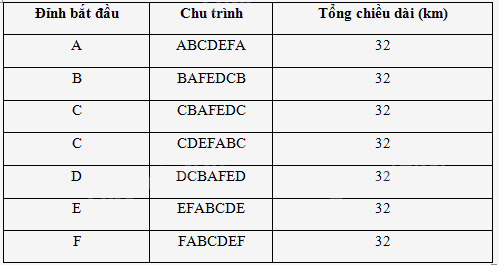
Vậy người giao hàng chọn 1 đường đi trong 7 đường đi trên thì quãng đường phải di chuyển là ngắn nhất.