Giải mục 2 trang 57, 58, 59, 60 Chuyên đề học tập Toán 11 - Cánh diều
Tổng quan nội dung
Giải mục 2 trang 57, 58, 59, 60 Chuyên đề học tập Toán 11 - Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 57, 58, 59, 60 của Chuyên đề học tập Toán 11 - Cánh Diều. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của các em.
Cho hình chóp tam giác đều O.ABC có các góc AOB, BOC, COA đều là góc vuông.
Luyện tập 3
Hãy xác định hình chiếu trục đo vuông góc đều của những hình tròn nằm trong các mặt phẳng song song với các mặt phẳng tọa độ.
Phương pháp giải:
Giả sử một vật thể gắn hệ trục tọa độ vuông góc OXYZ với các trục tọa độ đặt theo chiều dài, chiều rộng và chiều cao của vật thể. Chiếu vật thể cùng hệ tọa độ vuông góc lên mặt phẳng hình chiếu (P’) theo phương l (l không song song với (P’) và không song song với các trục tọa độ). Kết uqr trên mặt phẳng (P’) nhận được một hình chiếu của vật thể và hệ tọa độ O’X’Y’Z’. Hình biểu diễn đó gọi là hình chiếu trục đo của vật thể.
Lời giải chi tiết:
Hình chiếu trục đo vuông góc đều của hình tròn nằm trong các mặt phẳng song song với các mặt tọa độ là hình elip theo các hướng khác nhau.
Trong hình chiếu trục đo vuông góc đều tỉ số biến dạng được quy ước: Nếu vẽ theo hệ số biến dạng quy ước (p = q = r = 1) thì các elip đó có trục dài bằng 1,22d và trục ngắn bằng 0,71d (với d là đường kính của đường tròn).
Góc trục đo hình chiếu trục đo của hình tròn:
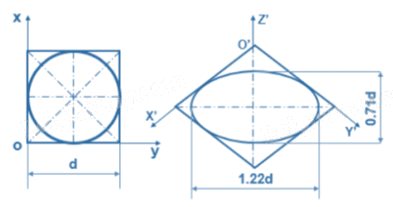
Hướng các elip:
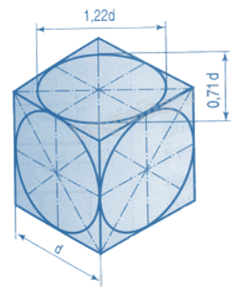
Hoạt động 4
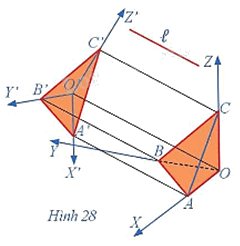
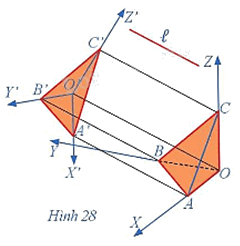
Trong Hoạt động 3, giả sử đường thẳng ℓ vuông góc với mặt phẳng (P') (Hình 28).
a) Tam giác A'B'C' có phải là tam giác đều hay không?
b) Tìm số đo của các góc trục đo: \(\widehat {X'O'Y'};\,\,\widehat {Y'O'Z'};\,\,\widehat {Z'O'X'}\).
c) So sánh các hệ số biến dạng: \(p = \frac{{O'A'}}{{OA}};\,q = \frac{{O'B'}}{{OB}};\,r = \frac{{O'C'}}{{OC}}\)
Phương pháp giải:
- Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc 3 góc bằng nhau.
- Quan sát hình 28, 29 để trả lời.
Lời giải chi tiết:
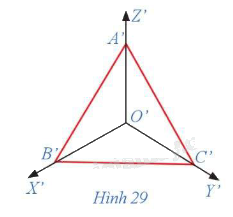
a) Tam giác A'B'C' là tam giác đều.
b) \(\widehat {X'O'Y'} = \,\,\widehat {Y'O'Z'} = \,\widehat {Z'O'X'} = 120^\circ \)
c) Ta có: \(p{\rm{ }} = {\rm{ }}q{\rm{ }} = {\rm{ }}r{\rm{ }} = {\rm{ }}1.\)
Hoạt động 3
Cho hình chóp tam giác đều O.ABC có các góc AOB, BOC, COA đều là góc vuông. Xét hệ trục tọa độ vuông góc OXYZ sao cho A, B, C lần lượt nằm trên các trục OX, OY, OZ. Gọi (P) là mặt phẳng đi qua ba điểm A, B, C và (P') là mặt phẳng song song với mặt phẳng (P).
Giả sử ℓ là đường thẳng không song song với (P') và không song song với các trục tọa độ, các điểm O', A', B', C' lần lượt là hình chiếu song song theo phương ℓ của các điểm O, A, B, C trên mặt phẳng (P') (Hình 25).
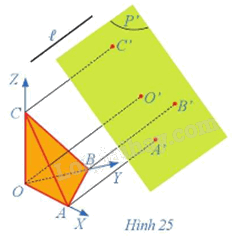
Hãy xác định:
a) Hình chiếu song song O'X', O'Y', O'Z' trên mặt phẳng (P') của lần lượt các trục tọa độ OX, OY, OZ theo phương ℓ;
b) Hình chiếu song song theo phương ℓ của hình chóp tam giác đều O.ABC trên mặt phẳng (P').
Phương pháp giải:
Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) sao cho MM’ song song hoặc trùng với \(l\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
Lời giải chi tiết:
a) Hình chiếu song song O'X', O'Y', O'Z' trên mặt phẳng (P') của lần lượt các trục tọa độ OX, OY, OZ theo phương ℓ là tia OA', OB', OC'.
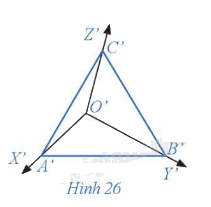
b) Hình chiếu song song theo phương ℓ của hình chóp tam giác đều O.ABC trên mặt phẳng (P') là tam giác A'B'C'.
- Hoạt động 3
- Hoạt động 4
- Luyện tập 3
Cho hình chóp tam giác đều O.ABC có các góc AOB, BOC, COA đều là góc vuông. Xét hệ trục tọa độ vuông góc OXYZ sao cho A, B, C lần lượt nằm trên các trục OX, OY, OZ. Gọi (P) là mặt phẳng đi qua ba điểm A, B, C và (P') là mặt phẳng song song với mặt phẳng (P).
Giả sử ℓ là đường thẳng không song song với (P') và không song song với các trục tọa độ, các điểm O', A', B', C' lần lượt là hình chiếu song song theo phương ℓ của các điểm O, A, B, C trên mặt phẳng (P') (Hình 25).
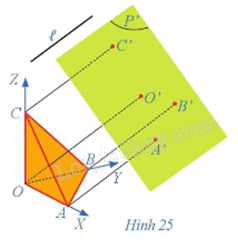
Hãy xác định:
a) Hình chiếu song song O'X', O'Y', O'Z' trên mặt phẳng (P') của lần lượt các trục tọa độ OX, OY, OZ theo phương ℓ;
b) Hình chiếu song song theo phương ℓ của hình chóp tam giác đều O.ABC trên mặt phẳng (P').
Phương pháp giải:
Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) sao cho MM’ song song hoặc trùng với \(l\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
Lời giải chi tiết:
a) Hình chiếu song song O'X', O'Y', O'Z' trên mặt phẳng (P') của lần lượt các trục tọa độ OX, OY, OZ theo phương ℓ là tia OA', OB', OC'.
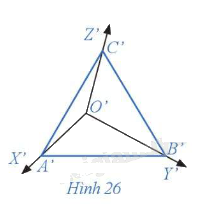
b) Hình chiếu song song theo phương ℓ của hình chóp tam giác đều O.ABC trên mặt phẳng (P') là tam giác A'B'C'.
Trong Hoạt động 3, giả sử đường thẳng ℓ vuông góc với mặt phẳng (P') (Hình 28).
a) Tam giác A'B'C' có phải là tam giác đều hay không?
b) Tìm số đo của các góc trục đo: \(\widehat {X'O'Y'};\,\,\widehat {Y'O'Z'};\,\,\widehat {Z'O'X'}\).
c) So sánh các hệ số biến dạng: \(p = \frac{{O'A'}}{{OA}};\,q = \frac{{O'B'}}{{OB}};\,r = \frac{{O'C'}}{{OC}}\)
Phương pháp giải:
- Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc 3 góc bằng nhau.
- Quan sát hình 28, 29 để trả lời.
Lời giải chi tiết:
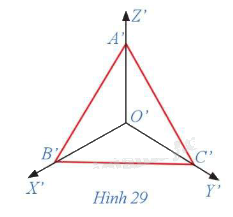
a) Tam giác A'B'C' là tam giác đều.
b) \(\widehat {X'O'Y'} = \,\,\widehat {Y'O'Z'} = \,\widehat {Z'O'X'} = 120^\circ \)
c) Ta có: \(p{\rm{ }} = {\rm{ }}q{\rm{ }} = {\rm{ }}r{\rm{ }} = {\rm{ }}1.\)
Hãy xác định hình chiếu trục đo vuông góc đều của những hình tròn nằm trong các mặt phẳng song song với các mặt phẳng tọa độ.
Phương pháp giải:
Giả sử một vật thể gắn hệ trục tọa độ vuông góc OXYZ với các trục tọa độ đặt theo chiều dài, chiều rộng và chiều cao của vật thể. Chiếu vật thể cùng hệ tọa độ vuông góc lên mặt phẳng hình chiếu (P’) theo phương l (l không song song với (P’) và không song song với các trục tọa độ). Kết uqr trên mặt phẳng (P’) nhận được một hình chiếu của vật thể và hệ tọa độ O’X’Y’Z’. Hình biểu diễn đó gọi là hình chiếu trục đo của vật thể.
Lời giải chi tiết:
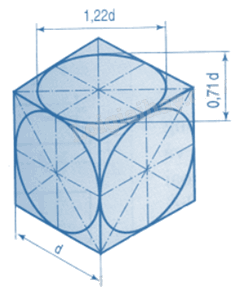
Hình chiếu trục đo vuông góc đều của hình tròn nằm trong các mặt phẳng song song với các mặt tọa độ là hình elip theo các hướng khác nhau.
Trong hình chiếu trục đo vuông góc đều tỉ số biến dạng được quy ước: Nếu vẽ theo hệ số biến dạng quy ước (p = q = r = 1) thì các elip đó có trục dài bằng 1,22d và trục ngắn bằng 0,71d (với d là đường kính của đường tròn).
Góc trục đo hình chiếu trục đo của hình tròn:
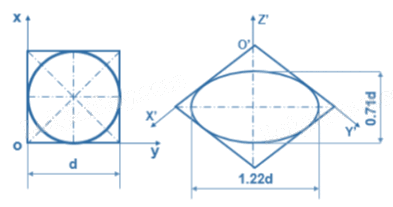
Hướng các elip:
Giải mục 2 trang 57, 58, 59, 60 Chuyên đề học tập Toán 11 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu
Mục 2 của Chuyên đề học tập Toán 11 - Cánh Diều thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trong mục này không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề.
Nội dung chính của Mục 2
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định rõ các nội dung chính mà nó đề cập đến. Thông thường, mục này sẽ bao gồm:
- Lý thuyết trọng tâm: Tóm tắt các định nghĩa, định lý, công thức quan trọng liên quan đến chủ đề.
- Ví dụ minh họa: Các bài toán mẫu được giải chi tiết để giúp học sinh hiểu rõ phương pháp giải.
- Bài tập áp dụng: Các bài tập với mức độ khó tăng dần để học sinh luyện tập và củng cố kiến thức.
Giải chi tiết các bài tập trang 57
Bài 1: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Bài 2: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Bài 3: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Giải chi tiết các bài tập trang 58
Bài 4: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Bài 5: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Giải chi tiết các bài tập trang 59
Bài 6: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Bài 7: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Giải chi tiết các bài tập trang 60
Bài 8: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Bài 9: (Nêu lại đề bài). Giải: (Giải chi tiết bài toán, kèm theo giải thích từng bước).
Mẹo giải toán hiệu quả
Để giải các bài tập Toán 11 - Cánh Diều một cách hiệu quả, các em nên:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán.
- Vận dụng lý thuyết: Sử dụng các định nghĩa, định lý, công thức đã học để giải bài toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả của mình là chính xác.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
Tusach.vn - Đồng hành cùng học sinh
Tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và sách bài tập Toán 11 - Cánh Diều. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất!
| Chủ đề | Trang |
|---|---|
| Mục 2 | 57-60 |