Giải bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này cung cấp phương pháp giải bài tập, đáp án chính xác và giải thích rõ ràng để giúp học sinh hiểu sâu kiến thức.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em.
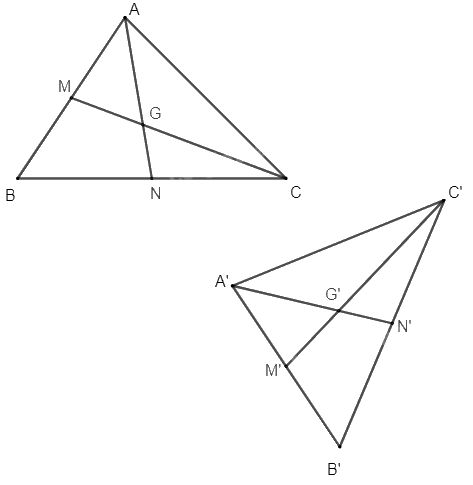
Chứng minh rằng nếu phép dời hình F biến tam giác ABC thành tam giác A'B'C' thì F lần lượt biến trọng tâm, trực tâm
Giải bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan và Phương pháp
Bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung chi tiết bài 15 trang 25
Bài 15 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số.
- Dạng 2: Tìm cực trị của hàm số.
- Dạng 3: Khảo sát sự biến thiên của hàm số.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán tối ưu.
Lời giải chi tiết từng phần của bài 15
Phần 1: Tính đạo hàm
Để tính đạo hàm của hàm số, ta cần áp dụng các quy tắc tính đạo hàm đã học, bao gồm:
- Quy tắc đạo hàm của tổng, hiệu, tích, thương.
- Quy tắc đạo hàm của hàm hợp.
- Đạo hàm của các hàm số cơ bản (hàm số mũ, hàm số logarit, hàm lượng giác).
Ví dụ, cho hàm số y = x2 + 2x + 1. Ta có y' = 2x + 2.
Phần 2: Tìm cực trị của hàm số
Để tìm cực trị của hàm số, ta thực hiện các bước sau:
- Tính đạo hàm y'.
- Giải phương trình y' = 0 để tìm các điểm cực trị.
- Xác định loại cực trị (cực đại hoặc cực tiểu) bằng cách xét dấu đạo hàm cấp hai y'' hoặc sử dụng phương pháp xét dấu đạo hàm y' trên các khoảng xác định.
Ví dụ, cho hàm số y = x3 - 3x + 2. Ta có y' = 3x2 - 3. Giải phương trình y' = 0, ta được x = 1 hoặc x = -1. y'' = 6x. Tại x = 1, y'' = 6 > 0, hàm số đạt cực tiểu. Tại x = -1, y'' = -6 < 0, hàm số đạt cực đại.
Phần 3: Khảo sát sự biến thiên của hàm số
Để khảo sát sự biến thiên của hàm số, ta thực hiện các bước sau:
- Xác định tập xác định của hàm số.
- Tính đạo hàm y'.
- Tìm các điểm cực trị.
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm giới hạn của hàm số khi x tiến tới vô cùng và các điểm bất thường.
- Vẽ đồ thị hàm số.
Phần 4: Ứng dụng đạo hàm để giải các bài toán tối ưu
Đạo hàm được sử dụng để giải các bài toán tối ưu bằng cách tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số trên một khoảng xác định. Ví dụ, tìm giá trị lớn nhất của diện tích hình chữ nhật nội tiếp trong một đường tròn.
Lưu ý khi giải bài tập
Khi giải bài tập về đạo hàm, cần lưu ý:
- Nắm vững các quy tắc tính đạo hàm.
- Kiểm tra kỹ kết quả tính đạo hàm.
- Sử dụng đạo hàm cấp hai để xác định loại cực trị.
- Phân tích kỹ đề bài để lựa chọn phương pháp giải phù hợp.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác các bài tập trong sách giáo khoa Toán 11 Cánh diều. Hãy truy cập tusach.vn để học Toán 11 hiệu quả và đạt kết quả tốt nhất!