Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Tổng quan nội dung
Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 23 trong Chuyên đề học tập Toán 11 của nhà xuất bản Cánh diều. Chúng tôi sẽ đi qua từng bước giải, giải thích rõ ràng các khái niệm và công thức liên quan.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Phép đối xứng tâm có là phép quay hay không? Vì sao?
Đề bài
Phép đối xứng tâm có là phép quay hay không? Vì sao?
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức:
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({D_O}\). Điểm O được gọi là tâm đối xứng.
- Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết
Phép đối xứng tâm là phép quay.
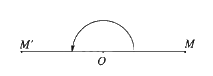
Thật vậy, cho điểm O, với mỗi điểm M, ta có M' là ảnh của điểm M qua phép đối xứng tâm O khi O là trung điểm của đoạn thẳng MM', suy ra \(OM{\rm{ }} = {\rm{ }}OM'\) và \(\widehat {MOM'} = 180^\circ \).
Khi đó góc lượng giác \(\;\left( {OM;{\rm{ }}OM'} \right)\) có số đo bằng (2k + 1)π và \(OM{\rm{ }} = {\rm{ }}OM'\)nên ta có phép quay tâm O, góc quay \(\left( {2k + 1} \right)\pi \) biến điểm M thành điểm M'.
Vậy phép đối xứng tâm O là phép quay \({Q_{(O,{\rm{ }}\left( {2k{\rm{ }} + {\rm{ }}1} \right)\pi )}}.\)
Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan và Phương pháp
Bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều thường tập trung vào một trong các chủ đề chính của chương, ví dụ như hàm số lượng giác, phương trình lượng giác, hoặc các bài toán về vectơ. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững kiến thức cơ bản về lý thuyết, các công thức và phương pháp giải liên quan.
Các bước giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và những điều cần tìm.
- Xác định kiến thức liên quan: Nhận diện các khái niệm, định lý, công thức nào cần sử dụng để giải bài toán.
- Lập kế hoạch giải: Phân tích bài toán và đưa ra các bước giải cụ thể.
- Thực hiện giải: Áp dụng kiến thức và kế hoạch giải để tìm ra đáp án.
- Kiểm tra lại kết quả: Đảm bảo đáp án tìm được thỏa mãn các điều kiện của bài toán và có ý nghĩa thực tế.
Giải chi tiết bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều (Ví dụ)
Để minh họa, chúng ta sẽ xem xét một ví dụ cụ thể về bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều. Giả sử bài toán yêu cầu giải phương trình lượng giác:
sin(2x) = cos(x)
Lời giải
Ta có thể biến đổi phương trình như sau:
sin(2x) = cos(x)2sin(x)cos(x) = cos(x)2sin(x)cos(x) - cos(x) = 0cos(x)(2sin(x) - 1) = 0
Từ đó, ta có hai trường hợp:
cos(x) = 0=>x = π/2 + kπ, k ∈ Z2sin(x) - 1 = 0=>sin(x) = 1/2=>x = π/6 + k2π hoặc x = 5π/6 + k2π, k ∈ Z
Vậy nghiệm của phương trình là: x = π/2 + kπ, x = π/6 + k2π, x = 5π/6 + k2π, k ∈ Z
Mẹo và Lưu ý khi giải bài tập Toán 11 Cánh diều
- Nắm vững lý thuyết: Đảm bảo bạn hiểu rõ các định nghĩa, định lý và công thức liên quan.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị có thể giúp bạn giải quyết các bài toán phức tạp.
- Tham khảo các nguồn tài liệu: Sách giáo khoa, sách bài tập, các trang web học tập trực tuyến là những nguồn tài liệu hữu ích.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn cung cấp đầy đủ các giải bài tập Toán 11 Cánh diều, đáp án chi tiết và dễ hiểu. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các tài liệu học tập chất lượng cao. Hãy truy cập tusach.vn để học Toán 11 hiệu quả và đạt kết quả tốt nhất!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 11 Cánh diều | https://tusach.vn |
| Đáp án Toán 11 Cánh diều | https://tusach.vn |