Giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Tổng quan nội dung
Giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, hỗ trợ tối đa cho quá trình học tập của các bạn.
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
Đề bài
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
a) Trung điểm các cạnh AB, BC, CD, DA;
b) Các đường thẳng AB, AC.
Phương pháp giải - Xem chi tiết
Dựa vào phép đối xứng tâm:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({D_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết
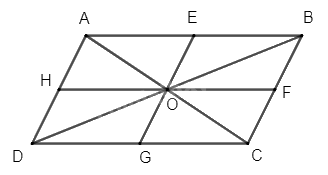
a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có E và O lần lượt là trung điểm của AB và AC nên OE là đường trung bình của tam giác ABC, suy ra OE // BC và \(OE = \frac{1}{2}BC\,\,(1)\)
Xét tam giác DBC có O và G lần lượt là trung điểm của DB và DC nên OG là đường trung bình của tam giác DBC, suy ra OG // BC và \(OG = \frac{1}{2}BC\,\,(2)\)
Từ (1) và (2) suy ra E, O, G thẳng hàng và OE = OG. Do đó, O là trung điểm của EG.
Chứng minh tương tự ta được O là trung điểm của HF.
Như vậy, ảnh của các điểm E, F, G, H qua phép đối xứng tâm O lần lượt là các điểm G, H, E, F.
b) Vì O là trung điểm của AC và BD nên ta có phép đối xứng tâm O biến các điểm A, B, C thành các điểm C, D, A.
Do đó, phép đối xứng tâm O biến đường thẳng AB thành đường thẳng CD, biến đường thẳng AC thành đường thẳng CA (chính nó).
Giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều: Chi tiết và Dễ hiểu
Bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giúp các em học sinh nắm vững kiến thức và tự tin làm bài, Tusach.vn xin trình bày lời giải chi tiết bài tập này.
Nội dung bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Bài 4 yêu cầu học sinh giải các bài toán liên quan đến việc tìm đạo hàm của hàm số, xét tính đơn điệu của hàm số và tìm cực trị của hàm số. Cụ thể, bài tập thường bao gồm:
- Tính đạo hàm của hàm số cho trước.
- Tìm tập xác định của hàm số.
- Xác định các điểm mà hàm số không có đạo hàm.
- Giải các phương trình đạo hàm bằng 0 để tìm các điểm cực trị.
- Xác định khoảng đồng biến và nghịch biến của hàm số.
Lời giải chi tiết bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Để giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều, chúng ta cần nắm vững các kiến thức sau:
- Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
- Đạo hàm của hàm hợp: Biết cách tính đạo hàm của hàm hợp bằng quy tắc chuỗi.
- Điều kiện cực trị: Nắm vững điều kiện cần và đủ để hàm số có cực trị.
- Khảo sát hàm số: Biết cách khảo sát hàm số bằng đạo hàm để xác định khoảng đồng biến, nghịch biến và cực trị.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tìm đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1. Ta thực hiện như sau:
f'(x) = 3x2 + 4x - 5
Mẹo giải bài tập đạo hàm hiệu quả
- Nắm vững lý thuyết: Đây là nền tảng quan trọng để giải quyết mọi bài toán.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng công cụ hỗ trợ: Các công cụ tính đạo hàm online có thể giúp bạn kiểm tra lại kết quả.
- Kiểm tra lại kết quả: Luôn kiểm tra lại kết quả để đảm bảo tính chính xác.
Tại sao nên chọn Tusach.vn để học Toán 11?
Tusach.vn là địa chỉ tin cậy cho các em học sinh học Toán 11. Chúng tôi cung cấp:
- Lời giải chi tiết, dễ hiểu: Các bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức.
- Đội ngũ giáo viên giàu kinh nghiệm: Các bài giải được biên soạn bởi các giáo viên có nhiều năm kinh nghiệm trong giảng dạy Toán.
- Cập nhật liên tục: Nội dung được cập nhật thường xuyên, đảm bảo tính chính xác và phù hợp với chương trình học.
- Giao diện thân thiện, dễ sử dụng: Website được thiết kế trực quan, giúp học sinh dễ dàng tìm kiếm thông tin.
Hy vọng với lời giải chi tiết bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều này, các em học sinh sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán. Chúc các em thành công!
| Chủ đề | Nội dung |
|---|---|
| Đạo hàm | Quy tắc tính đạo hàm, đạo hàm của hàm hợp |
| Tính đơn điệu | Xác định khoảng đồng biến, nghịch biến |
| Cực trị | Tìm cực đại, cực tiểu |