Giải mục 3 trang 10, 11, 12, 13 Chuyên đề học tập Toán 11 - Cánh diều
Tổng quan nội dung
Giải mục 3 trang 10, 11, 12, 13 Chuyên đề học tập Toán 11 - Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 10, 11, 12, 13 của Chuyên đề học tập Toán 11, bộ sách Cánh Diều. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của các em.
Trong mặt phẳng cho đường thẳng d.
Luyện tập 5
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng trục, sau đó viết phương trình đường tròn (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng trục Ox là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Ta có I' là ảnh của I qua phép đối xứng trục Ox, suy ra I'(3; – 2). Vậy ảnh của đường tròn (C) qua phép đối xứng trục Ox là đường tròn (C') có tâm I'(3; – 2), bán kính R' = 2.
Hoạt động 6
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng trục Ox.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Với mỗi điểm M(x1; y1) ta có M'(x1'; y1') là ảnh của điểm M qua phép đối xứng trục Ox thì \(\left\{ {\begin{array}{*{20}{l}}{{x_1}' = {x_1}}\\{{y_1}' = - {y_1}}\end{array}} \right.\)
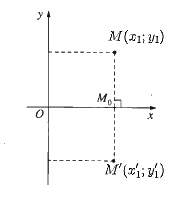
Do đó M'(x1; – y1) và N'(x2; – y2).
b) Ta có
\(\begin{array}{l}MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \\M'N' = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {\left( { - {y_2}} \right) - \left( { - {y_1}} \right)} \right)}^2}} \end{array}\)
Từ đó suy ra MN = M'N'.
Luyện tập 4
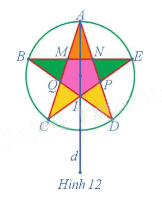
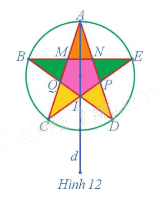
Xác định ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
Ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12 là cánh sao màu vàng có các đỉnh C, I, Q.
Luyện tập 3
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
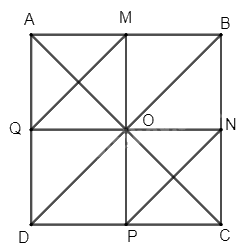
Gọi O là giao điểm hai đường chéo AC và BD của hình vuông ABCD.
Khi đó O là trung điểm của AC và BD. Ta chứng minh được O cũng là trung điểm của MP và QN. Lại có MP = QN = AB = BC = CD = DA nên ta suy ra OM = OQ = OP = ON = MA = MB = NB = NC = PC = PD = QD = QA.
+ Ta có AQ = AM và OQ = OM nên AO là đường trung trực của đoạn thẳng QM hay AC là đường trung trực của đoạn thẳng QM. Tương tự, ta chứng minh được AC là đường trung trực của đoạn thẳng PN.
Do đó, ta có phép đối xứng trục AC biến các điểm M, N, P, Q tương ứng thành các điểm Q, P, N, M.
Vậy ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC lần lượt là các điểm Q, P, N, M.
Hoạt động 5
Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M trong mặt phẳng và M ∉ d, hãy xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua đường thẳng d) (Hình 9).
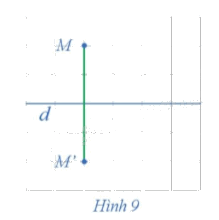
Phương pháp giải:
Đường trung trực là đường đi qua trung điểm đoạn thẳng và vuông góc với đoạn thẳng tại trung điểm.
Lời giải chi tiết:
Cách xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM':
- Qua M kẻ đường thẳng d' vuông góc với đường thẳng d tại H.
- Trên d', lấy điểm M' sao cho MH = M'H.
Khi đó đường thẳng d vuông góc với MM' tại trung điểm H của MM' nên d là đường trung trực của đoạn thẳng MM'.
Hoạt động 8
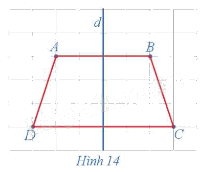
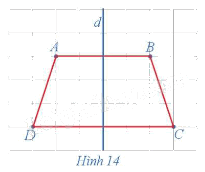
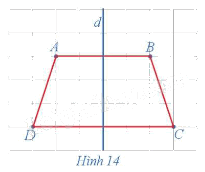
Trong mặt phẳng, cho hình thang cân ABCD, kí hiệu là ℋ. Gọi d là đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân đó (Hình 14).
Tìm ℋ' = Đd(ℋ).
Phương pháp giải:
Để tìm ảnh của (H) qua \(Đ_d\) ta tìm ảnh của các điểm thuococj (H) qua \(Đ_d\). Sau đó nối chúng với nhau.
Lời giải chi tiết:
Đường thẳng d đi qua trung điểm hai háy của hình thang cân ABCD nên đường thẳng d là đường trung trực của các đoạn thẳng AB và CD.
Khi đó, ta có phép đối xứng trục d biến các điểm A, B, C, D tương ứng thành các điểm B, A, D, C nên phép đối xứng trục d biến hình thang cân ABCD thành hình thang cân BADC hay hình thang cân ABCD là ảnh của chính nó qua phép đối xứng trục d.
Như vậy, ℋ ' ≡ ℋ hay phép đối xứng trục d biến hình ℋ thành chính nó.
Hoạt động 7
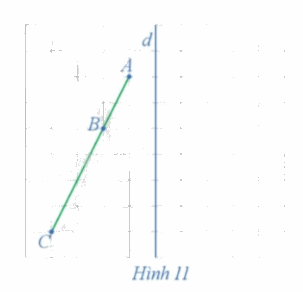
Xét phép đối xứng trục d (Hình 11)
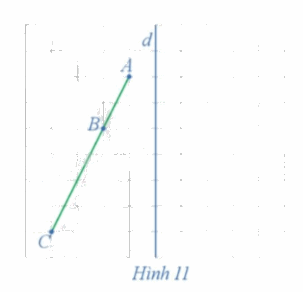
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d như trên hình vẽ dưới đây.
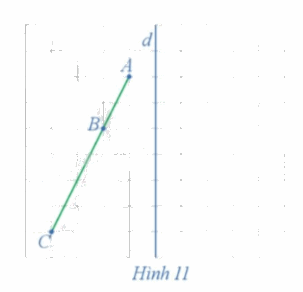
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
- Hoạt động 5
- Luyện tập 3
- Hoạt động 6
- Hoạt động 7
- Luyện tập 4
- Luyện tập 5
- Hoạt động 8
Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M trong mặt phẳng và M ∉ d, hãy xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua đường thẳng d) (Hình 9).
Phương pháp giải:
Đường trung trực là đường đi qua trung điểm đoạn thẳng và vuông góc với đoạn thẳng tại trung điểm.
Lời giải chi tiết:
Cách xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM':
- Qua M kẻ đường thẳng d' vuông góc với đường thẳng d tại H.
- Trên d', lấy điểm M' sao cho MH = M'H.
Khi đó đường thẳng d vuông góc với MM' tại trung điểm H của MM' nên d là đường trung trực của đoạn thẳng MM'.
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
Gọi O là giao điểm hai đường chéo AC và BD của hình vuông ABCD.
Khi đó O là trung điểm của AC và BD. Ta chứng minh được O cũng là trung điểm của MP và QN. Lại có MP = QN = AB = BC = CD = DA nên ta suy ra OM = OQ = OP = ON = MA = MB = NB = NC = PC = PD = QD = QA.
+ Ta có AQ = AM và OQ = OM nên AO là đường trung trực của đoạn thẳng QM hay AC là đường trung trực của đoạn thẳng QM. Tương tự, ta chứng minh được AC là đường trung trực của đoạn thẳng PN.
Do đó, ta có phép đối xứng trục AC biến các điểm M, N, P, Q tương ứng thành các điểm Q, P, N, M.
Vậy ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC lần lượt là các điểm Q, P, N, M.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng trục Ox.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Với mỗi điểm M(x1; y1) ta có M'(x1'; y1') là ảnh của điểm M qua phép đối xứng trục Ox thì \(\left\{ {\begin{array}{*{20}{l}}{{x_1}' = {x_1}}\\{{y_1}' = - {y_1}}\end{array}} \right.\)
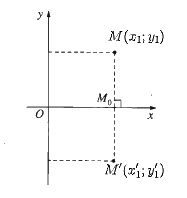
Do đó M'(x1; – y1) và N'(x2; – y2).
b) Ta có
\(\begin{array}{l}MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \\M'N' = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {\left( { - {y_2}} \right) - \left( { - {y_1}} \right)} \right)}^2}} \end{array}\)
Từ đó suy ra MN = M'N'.
Xét phép đối xứng trục d (Hình 11)
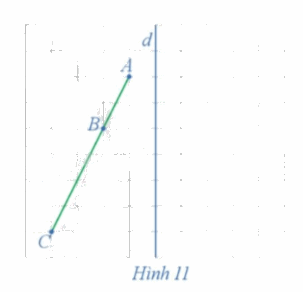
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d như trên hình vẽ dưới đây.
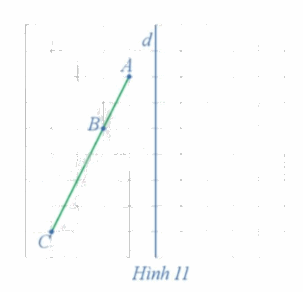
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Xác định ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
Ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12 là cánh sao màu vàng có các đỉnh C, I, Q.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng trục, sau đó viết phương trình đường tròn (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng trục Ox là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Ta có I' là ảnh của I qua phép đối xứng trục Ox, suy ra I'(3; – 2). Vậy ảnh của đường tròn (C) qua phép đối xứng trục Ox là đường tròn (C') có tâm I'(3; – 2), bán kính R' = 2.
Trong mặt phẳng, cho hình thang cân ABCD, kí hiệu là ℋ. Gọi d là đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân đó (Hình 14).
Tìm ℋ' = Đd(ℋ).
Phương pháp giải:
Để tìm ảnh của (H) qua \(Đ_d\) ta tìm ảnh của các điểm thuococj (H) qua \(Đ_d\). Sau đó nối chúng với nhau.
Lời giải chi tiết:
Đường thẳng d đi qua trung điểm hai háy của hình thang cân ABCD nên đường thẳng d là đường trung trực của các đoạn thẳng AB và CD.
Khi đó, ta có phép đối xứng trục d biến các điểm A, B, C, D tương ứng thành các điểm B, A, D, C nên phép đối xứng trục d biến hình thang cân ABCD thành hình thang cân BADC hay hình thang cân ABCD là ảnh của chính nó qua phép đối xứng trục d.
Như vậy, ℋ ' ≡ ℋ hay phép đối xứng trục d biến hình ℋ thành chính nó.
Giải mục 3 trang 10, 11, 12, 13 Chuyên đề học tập Toán 11 - Cánh Diều: Tổng quan và hướng dẫn chi tiết
Mục 3 trong Chuyên đề học tập Toán 11 Cánh Diều thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trong mục này không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng vô cùng quan trọng trong học tập và cuộc sống.
Nội dung chính của Mục 3 (Trang 10, 11, 12, 13)
Để hiểu rõ hơn về Mục 3, chúng ta cần xác định chính xác nội dung mà nó bao gồm. Thông thường, các bài tập trong mục này sẽ xoay quanh các chủ đề sau (tùy thuộc vào chương cụ thể):
- Đạo hàm của hàm số lượng giác: Tính đạo hàm của các hàm số sin, cos, tan, cot và các hàm hợp.
- Ứng dụng đạo hàm để khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số.
- Bài toán tối ưu: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
- Phương trình lượng giác: Giải các phương trình lượng giác cơ bản và nâng cao.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 3 trang 10, 11, 12, 13 Chuyên đề học tập Toán 11 Cánh Diều:
Bài 1: Tính đạo hàm của hàm số y = sin(2x)
Lời giải:
- Sử dụng công thức đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x)
- Đặt u(v) = sin(v) và v(x) = 2x
- Khi đó, u'(v) = cos(v) và v'(x) = 2
- Vậy, y' = cos(2x) * 2 = 2cos(2x)
Bài 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Lời giải:
- Tính đạo hàm bậc nhất: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0 => 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Tính đạo hàm bậc hai: y'' = 6x - 6
- Kiểm tra dấu của đạo hàm bậc hai tại các điểm dừng:
- y''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0, ymax = 2
- y''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, ymin = -2
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong Mục 3 một cách nhanh chóng và hiệu quả, các em có thể tham khảo một số mẹo sau:
- Nắm vững các công thức đạo hàm cơ bản: Điều này sẽ giúp các em tiết kiệm thời gian và tránh sai sót.
- Sử dụng các quy tắc đạo hàm: Quy tắc tích, quy tắc thương, quy tắc hàm hợp là những công cụ hữu ích để tính đạo hàm của các hàm số phức tạp.
- Vẽ đồ thị hàm số: Đồ thị hàm số sẽ giúp các em hình dung rõ hơn về tính chất của hàm số và tìm ra các điểm cực trị.
- Luyện tập thường xuyên: Không có cách nào tốt hơn để nắm vững kiến thức và kỹ năng giải bài tập bằng việc luyện tập thường xuyên.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
- Sách bài tập Toán 11: Cung cấp nhiều bài tập đa dạng và phong phú để các em luyện tập.
- Các trang web học Toán trực tuyến: Tusach.vn, Vietjack, Loigiaihay,...
- Các video bài giảng Toán 11 trên YouTube: Giúp các em hiểu rõ hơn về lý thuyết và phương pháp giải bài tập.
Hy vọng với những hướng dẫn chi tiết và hữu ích trên, các em sẽ tự tin chinh phục Mục 3 trang 10, 11, 12, 13 Chuyên đề học tập Toán 11 Cánh Diều. Chúc các em học tốt!