Giải bài 1 trang 32 Chuyên đề học tập Toán 11 Cánh diều
Tổng quan nội dung
Giải bài 1 trang 32 Chuyên đề học tập Toán 11 Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 1 trang 32 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Cánh diều, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
Phép biến hình nào trong các phép biến hình dưới đây là phép vị tự?
Đề bài
Phép biến hình nào trong các phép biến hình dưới đây là phép vị tự?
a) Phép tịnh tiến theo vectơ khác \(\vec 0\);
b) Phép đối xứng tâm;
c) Phép đối xứng trục;
d) Phép quay.
Phương pháp giải - Xem chi tiết
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết
a) Phép tịnh tiến theo vectơ khác \(\overrightarrow 0 \) không phải là phép vị tự vì không có điểm nào biến thành chính nó.
b) Phép đối xứng tâm là phép vị tự với tâm là tâm đối xứng và tỉ số k = – 1.
Chứng minh:
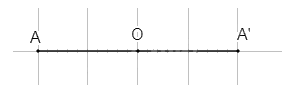
Giả sử ta có phép đối xứng tâm O biến điểm A thành điểm A', khi đó O là trung điểm của AA', suy ra \(\overrightarrow {OA'} = - \overrightarrow {OA} \), do đó ta có phép vị tự tâm O tỉ số – 1 biến điểm A thành A'.
c) Phép đối xứng trục không phải là phép vị tự vì các đường thẳng nối cặp điểm tương ứng không đồng quy.
d) Phép quay với tâm O bất kì và góc quay \(\varphi = 2k\pi \) (chính là phép đồng nhất) là phép vị tự tâm O với tỉ số \(k = 1\).
Phép quay với tâm O bất kì và góc quay \(\varphi = \left( {2k{\rm{ }} + {\rm{ }}1} \right)\pi \) (chính là phép đối xứng tâm O) là phép vị tự tâm O với tỉ số \(k = -1\).
Phép quay với góc bất kì khác \(2k\pi ,{\rm{ }}\left( {2k + 1} \right)\pi \) không phải là phép vị tự.
Giải bài 1 trang 32 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan và Phương pháp giải
Bài 1 trang 32 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Nội dung chi tiết bài 1 trang 32
Bài 1 thường bao gồm các dạng bài tập sau:
- Xác định các hệ số a, b, c của hàm số bậc hai: Yêu cầu học sinh xác định đúng các hệ số này để phân tích và vẽ đồ thị hàm số.
- Tìm tập xác định và tập giá trị của hàm số: Học sinh cần nắm vững định nghĩa và phương pháp tìm tập xác định, tập giá trị của hàm số bậc hai.
- Tìm đỉnh, trục đối xứng và điểm đồng biến, nghịch biến của hàm số: Đây là những yếu tố quan trọng để vẽ đồ thị hàm số và phân tích tính chất của hàm số.
- Giải các bài toán ứng dụng liên quan đến hàm số bậc hai: Các bài toán này thường liên quan đến các tình huống thực tế, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết.
Lời giải chi tiết bài 1 trang 32 (Ví dụ)
Đề bài: Cho hàm số y = x2 - 4x + 3. Tìm đỉnh và trục đối xứng của parabol.
Lời giải:
- Xác định hệ số: a = 1, b = -4, c = 3
- Hoành độ đỉnh: xđỉnh = -b / (2a) = -(-4) / (2 * 1) = 2
- Tung độ đỉnh: yđỉnh = (2)2 - 4 * (2) + 3 = -1
- Đỉnh của parabol: I(2; -1)
- Trục đối xứng: x = 2
Mẹo giải bài tập hiệu quả
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, công thức và tính chất của hàm số bậc hai.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng công cụ hỗ trợ: Sử dụng máy tính bỏ túi hoặc các phần mềm vẽ đồ thị để kiểm tra kết quả và hiểu rõ hơn về hàm số.
- Tham khảo lời giải chi tiết: Nếu gặp khó khăn, hãy tham khảo lời giải chi tiết trên tusach.vn để hiểu rõ phương pháp giải.
Tại sao nên chọn tusach.vn để học Toán 11?
Tusach.vn là địa chỉ tin cậy cho học sinh và phụ huynh trong việc học tập và ôn luyện Toán 11. Chúng tôi cung cấp:
- Lời giải chi tiết, dễ hiểu: Đội ngũ giáo viên giàu kinh nghiệm biên soạn lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức.
- Cập nhật nhanh chóng: Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập mới nhất.
- Giao diện thân thiện: Website có giao diện thân thiện, dễ sử dụng, giúp học sinh tìm kiếm thông tin nhanh chóng và thuận tiện.
- Hỗ trợ nhiệt tình: Đội ngũ hỗ trợ luôn sẵn sàng giải đáp thắc mắc và hỗ trợ học sinh trong quá trình học tập.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và đạt kết quả cao trong môn Toán 11!