Giải bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều
Tổng quan nội dung
Giải bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu và cập nhật nhanh chóng nhất.
Hình 59 mô tả một viên gạch trang trí hình tam giác đều.
Đề bài
Hình 59 mô tả một viên gạch trang trí hình tam giác đều. Chứng minh rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.

Phương pháp giải - Xem chi tiết
- Phép biến hình F biến 2 điểm M, N bất kì thành 2 điểm M’, N’ sao cho \(M'N' = kMN\) với k là số thực dương cho trước, gọi là phép đồng dạng tỉ số k.
- Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết
Gọi viên gạch trang trí là ABC, giao của các canh hoa màu đỏ với BC, CA, AB lần lượt là các điểm D, E, F, G là tâm của hình tam giác đều, khi đó G là tâm của các hình hoa (quan sát hình vẽ dưới đây).
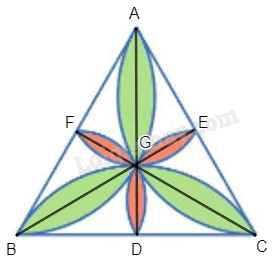
Qua phép quay tâm G, góc quay 120° hình cánh hoa màu xanh đỉnh A biến thành hình cánh hoa màu xanh đỉnh B, hình cánh hoa màu xanh đỉnh B biến thành hình cánh hoa màu xanh đỉnh C, hình cánh hoa màu đỏ đỉnh F biến thành hình cánh hoa màu đỏ đỉnh D, hình cánh hoa màu đỏ đỉnh D biến thành hình cánh hoa màu đỏ đỉnh E. Do đó, các hình cánh hoa màu xanh đồng dạng với nhau theo tỉ số 1 và các hình cánh hoa màu đỏ đồng dạng với nhau theo tỉ số 1 (phép dời hình là phép đồng dạng tỉ số 1).
Do đó, \(GA{\rm{ }} = {\rm{ }}GB{\rm{ }} = {\rm{ }}GC\) và \(GD{\rm{ }} = {\rm{ }}GE{\rm{ }} = {\rm{ }}GF\).
Ta có G là tâm của hình tam giác đều ABC nên G cũng là trọng tâm của tam giác ABC và D, E, F lần lượt là trung điểm của BC, CA, AB. Khi đó ta có: \(\overrightarrow {GD} = - \frac{1}{2}\overrightarrow {GA} ,\,\,\overrightarrow {GE} = - \frac{1}{2}\overrightarrow {GB} \) và \(\,\overrightarrow {GF} = - \frac{1}{2}\overrightarrow {GC} \) . Do đó, D, E, F lần lượt là ảnh của A, B, C qua phép vị tự tâm G, tỉ số \( - \frac{1}{2}\). Như vậy, khi ta lấy mỗi điểm bất kì trên hình hoa ba cánh màu xanh thì qua phép vị tự tâm G, tỉ số, điểm đó đều biến thành một điểm tương ứng trên hình hoa ba cánh màu đỏ. Vậy có phép đồng dạng biến hình hoa ba cánh màu xanh thành hình hoa ba cánh màu đỏ. Do đó, rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.
Giải bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan
Bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung chi tiết bài 12 trang 33
Bài 12 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số.
- Dạng 2: Tìm cực trị của hàm số.
- Dạng 3: Khảo sát hàm số bằng đạo hàm.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán tối ưu.
Lời giải chi tiết bài 12 trang 33
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 12 trang 33, Tusach.vn xin trình bày lời giải chi tiết cho từng câu hỏi:
Câu a: (Ví dụ minh họa)
Cho hàm số y = x3 - 3x2 + 2. Tính đạo hàm y' của hàm số.
Lời giải:
Áp dụng quy tắc tính đạo hàm của tổng và tích, ta có:
y' = 3x2 - 6x
Câu b: (Ví dụ minh họa)
Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Lời giải:
- Tính đạo hàm y' = 3x2 - 6x.
- Giải phương trình y' = 0 để tìm các điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
- Tính đạo hàm bậc hai y'' = 6x - 6.
- Xét dấu y'' tại các điểm cực trị:
- y''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0. Giá trị cực đại là y(0) = 2.
- y''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là y(2) = -2.
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, các em học sinh cần:
- Nắm vững các khái niệm cơ bản về đạo hàm.
- Thuộc các quy tắc tính đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
Tusach.vn – Đồng hành cùng học sinh
Tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các mẹo giải bài tập hiệu quả. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất!
| Dạng bài | Phương pháp giải |
|---|---|
| Tính đạo hàm | Sử dụng quy tắc tính đạo hàm của tổng, tích, thương, hàm hợp. |
| Tìm cực trị | Giải phương trình đạo hàm bằng 0, xét dấu đạo hàm bậc hai. |