Giải bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều
Tổng quan nội dung
Giải bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh.
Một nhân viên của bảo tàng nghệ thuật đang có kế hoạch giới thiệu nội dung cuộc triển lãm của bảo tàng đến ba trường học trong khu vực.
Đề bài
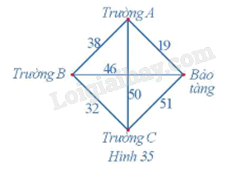
Một nhân viên của bảo tàng nghệ thuật đang có kế hoạch giới thiệu nội dung cuộc triển lãm của bảo tàng đến ba trường học trong khu vực. Người đó muốn đến từng trường và quay trở lại bảo tàng sau khi thăm cả ba trường. Thời gian di chuyển (đơn vị: phút) giữa các trường học và giữa bảo tàng với mỗi trường học được mô tả trong Hình 35.
Tìm chu trình xuất phát từ viện bảo tàng sao cho thời gian đi là ít nhất.
Phương pháp giải - Xem chi tiết
Bước 1. Chọn một đỉnh bắt đầu, ta gọi là đỉnh V.
Bước 2. Xuất phát từ đỉnh hiện hành, chọn cạnh có độ dài nhỏ nhất nối đến một trong các đỉnh chưa đến. Đánh dấu đỉnh cuối của cạnh vừa chọn.
Bước 3. Xuất phát từ đỉnh vừa đánh dấu, nếu còn đỉnh chưa đến thì quay lại bước 2.
Bước 4. Quay lại đỉnh V.
Lời giải chi tiết
Từ viện bảo tàng, thời gian di chuyển đến trường A là ngắn nhất: 19 phút.
Từ trường A, thời gian di chuyển đến trường B là ngắn nhất: 38 phút.
Từ trường B, thời gian di chuyển đến trường C là ngắn nhất: 32 phút.
Đến đây, không còn địa điểm nào chưa đi qua nên quay lại viện bảo tàng với thời gian di chuyển: 51 phút.
Do đó, chu trình xuất phát từ viện bảo tàng, qua trường A, trường B, trường C rồi quay lại viện bảo tàng có thời gian đi là ít nhất và thời gian đi là: 19 + 38 + 32 + 51 = 140 (phút).
Giải bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều: Hướng dẫn chi tiết
Bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, các quy tắc tính đạo hàm và cách sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều
Bài 5 thường yêu cầu học sinh thực hiện các nhiệm vụ sau:
- Tính đạo hàm của hàm số đã cho.
- Tìm tập xác định của hàm số.
- Xác định các điểm cực trị của hàm số.
- Khảo sát sự biến thiên của hàm số (khoảng đồng biến, nghịch biến).
- Vẽ đồ thị hàm số.
Lời giải chi tiết bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5 trang 49, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử hàm số được cho là:
f(x) = x3 - 3x2 + 2
Bước 1: Tính đạo hàm f'(x)
f'(x) = 3x2 - 6x
Bước 2: Tìm tập xác định của hàm số
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là R.
Bước 3: Tìm các điểm cực trị
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 4: Xác định loại cực trị
Ta xét dấu của f'(x) trên các khoảng:
- Khoảng (-∞, 0): f'(x) > 0, hàm số đồng biến.
- Khoảng (0, 2): f'(x) < 0, hàm số nghịch biến.
- Khoảng (2, +∞): f'(x) > 0, hàm số đồng biến.
Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Bước 5: Tính giá trị cực đại, cực tiểu
f(0) = 2 (cực đại)
f(2) = -2 (cực tiểu)
Mẹo giải bài tập đạo hàm và ứng dụng
Để giải các bài tập về đạo hàm và ứng dụng một cách hiệu quả, bạn nên:
- Nắm vững các công thức tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán để kiểm tra kết quả.
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
- Tìm cực trị của hàm số f(x) = x4 - 4x2 + 3
- Khảo sát sự biến thiên của hàm số f(x) = x3 + 3x2 - 9x + 5
Tusach.vn hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều và các bài tập tương tự. Chúc các em học tập tốt!