Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Tổng quan nội dung
Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC
Đề bài
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.
Phương pháp giải - Xem chi tiết
- Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
- Cần xác định vecto \(\overrightarrow u \).
Lời giải chi tiết
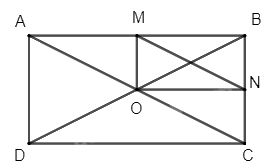
Vì O là giao điểm hai đường chéo của hình chữ nhật ABCD nên O là trung điểm của AC.
Suy ra \(\overrightarrow {AO} = \overrightarrow {OC} = \frac{1}{2}\overrightarrow {AC} \,\,(1)\)
Ta có M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và \(MN = \;\frac{1}{2}AC\). Do đó, \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \,\,(2)\)
Từ (1) và (2) suy ra \(\overrightarrow {AO} = \overrightarrow {OC} = \overrightarrow {MN} \).
Khi đó, ta có phép tịnh tiến theo vectơ \(\overrightarrow {AO} \) biến các điểm A, M, O lần lượt thành các điểm O, N, C.
Vậy phép tịnh tiến theo vectơ \(\overrightarrow {AO} \) biến tam giác AMO thành tam giác ONC.
Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan và Phương pháp giải
Bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Nội dung bài tập
Bài 1 thường bao gồm các dạng bài tập sau:
- Xác định các hệ số a, b, c của hàm số bậc hai.
- Tìm tập xác định và tập giá trị của hàm số.
- Xác định đỉnh, trục đối xứng và điểm đồng biến, nghịch biến của hàm số.
- Vẽ đồ thị hàm số.
- Giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Hướng dẫn giải chi tiết
Để giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Khái niệm hàm số bậc hai: Hàm số bậc hai có dạng y = ax2 + bx + c, trong đó a ≠ 0.
- Đỉnh của parabol: Tọa độ đỉnh của parabol là I( -b/2a ; (4ac - b2)/4a ).
- Trục đối xứng của parabol: Trục đối xứng của parabol là đường thẳng x = -b/2a.
- Điểm đồng biến, nghịch biến: Hàm số bậc hai đồng biến trên khoảng (-∞ ; -b/2a) nếu a > 0 và trên khoảng (-b/2a ; +∞) nếu a < 0. Hàm số bậc hai nghịch biến trên khoảng (-∞ ; -b/2a) nếu a < 0 và trên khoảng (-b/2a ; +∞) nếu a > 0.
Ví dụ minh họa
Bài toán: Cho hàm số y = 2x2 - 4x + 1. Hãy xác định đỉnh và trục đối xứng của parabol.
Giải:
Hệ số a = 2, b = -4, c = 1.
Tọa độ đỉnh của parabol là I( -(-4)/(2*2) ; (4*2*1 - (-4)2)/(4*2) ) = I( 1 ; -1 ).
Trục đối xứng của parabol là đường thẳng x = 1.
Lưu ý khi giải bài tập
- Đọc kỹ đề bài và xác định đúng yêu cầu của bài toán.
- Vận dụng linh hoạt các kiến thức đã học để giải quyết bài toán.
- Kiểm tra lại kết quả sau khi giải xong.
- Tham khảo các tài liệu học tập và bài giải mẫu để hiểu rõ hơn về cách giải bài tập.
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm sách giáo khoa, sách bài tập, đề thi và lời giải chi tiết. Chúng tôi cam kết mang đến cho các em những tài liệu học tập chất lượng, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
Bảng tổng hợp các dạng bài tập thường gặp
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định hệ số a, b, c | So sánh với dạng tổng quát y = ax2 + bx + c |
| Tìm tập xác định, tập giá trị | Phân tích hàm số và sử dụng kiến thức về tập số |
| Xác định đỉnh, trục đối xứng | Sử dụng công thức tính tọa độ đỉnh và phương trình trục đối xứng |
Hy vọng với những hướng dẫn chi tiết trên, các em sẽ tự tin giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều một cách dễ dàng. Chúc các em học tập tốt!