Giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
Tổng quan nội dung
Giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 73 trong Chuyên đề học tập Toán 11 của nhà xuất bản Cánh diều. Chúng tôi sẽ phân tích từng bước giải, cung cấp đáp án chính xác và giải thích rõ ràng các khái niệm liên quan.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi.
Đọc bản vẽ và khôi phục lại hình dạng của vật thể trong Hình 57, Hình 58.
Đề bài
Đọc bản vẽ và khôi phục lại hình dạng của vật thể trong Hình 57, Hình 58.
a) Vật thể: Gá mặt nghiêng;
b) Vật thể: Gá lỗ chữ nhật.
Phương pháp giải - Xem chi tiết
Quan sát hình 57, 58 để đọc bản vẽ.
Lời giải chi tiết
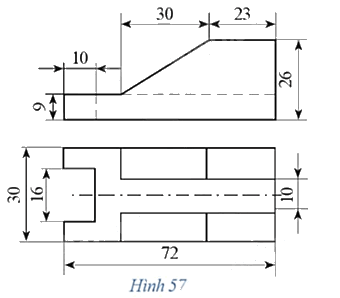
a) Đọc hai hình chiếu của gá mặt nghiêng ta thấy:
- Hình chiếu đứng có hai phần có kích thước khác nhau. Phần hình thang vuông phía trên có chiều cao 17, chiều rộng 53. Phần đế hình hộp chữ nhật phía dưới có chiều dài 72, chiều cao 9.
- Đối với hình chiếu bằng, ta thấy có hai hình chữ nhật và một khoảng trống 10 ở giữa tương ứng với phần hình thang vuông phía trên; hình chữ nhật bao ngoài tương ứng với phần đế phía dưới.
- Trên hình chiếu đứng có một nét đứt dọc tương ứng với rãnh chữ nhật ở hình chiếu bằng thể hiện phần khuyết trên đế hình hộp.
- Trên hình chiếu đứng còn có một nét đứt ngang tương ứng với chân hình thang vuông phía trên.
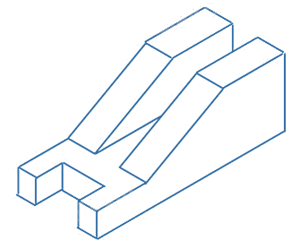
Từ đó hình dạng gá mặt nghiêng được biểu diễn như hình sau.
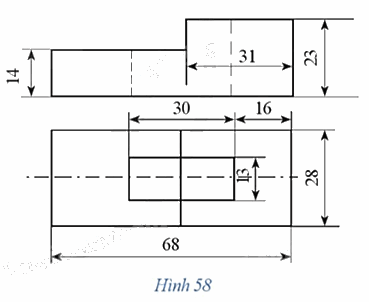
b) Đọc hai hình chiếu của gá lỗ chữ nhật ta thấy:
- Hình chiếu đứng hình chữ L nằm ngang. Chiều dài bao quát 68, chiều cao bao quát 23. Có hai phần: phần nhô cao có chiều dài 31, chiều cao 9; phần đế thấp có chiều cao 14.
- Hình chiếu bằng có hai hình chữ U và một hình chữ nhật rỗng ở giữa. Hình chữ U bên phải tương ứng với phần nhô cao ở hình chiếu đứng; hình chữ U bên trái tương ứng với phần đế thấp.
- Trên hình chiếu đứng có hai nét đứt tương ứng với hình chữ nhật rỗng ở giữa ở hình chiếu bằng thể hiện phần rỗng chữ nhật của gá.
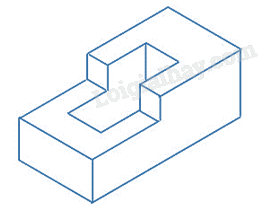
Từ đó hình dạng gá lỗ chữ nhật được biểu diễn như hình sau.
Giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan và Hướng dẫn chi tiết
Bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc tính đạo hàm, các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số và giải các bài toán tối ưu hóa.
Nội dung bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
Bài 2 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tìm đạo hàm của hàm số và xác định các điểm cực trị.
- Dạng 2: Khảo sát sự biến thiên của hàm số bằng đạo hàm.
- Dạng 3: Giải các bài toán tối ưu hóa (tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số).
Hướng dẫn giải chi tiết bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
Để giải quyết bài 2 trang 73 một cách hiệu quả, các em cần thực hiện theo các bước sau:
- Bước 1: Xác định hàm số cần khảo sát.
- Bước 2: Tính đạo hàm cấp nhất của hàm số.
- Bước 3: Tìm các điểm cực trị của hàm số bằng cách giải phương trình đạo hàm bằng 0.
- Bước 4: Lập bảng biến thiên của hàm số để xác định khoảng đồng biến, nghịch biến và các điểm cực trị.
- Bước 5: Giải các bài toán tối ưu hóa (nếu có) bằng cách sử dụng đạo hàm.
Ví dụ minh họa giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
Bài toán: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Giải:
- Tính đạo hàm cấp nhất: y' = 3x2 - 6x
- Tìm các điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
- Xác định loại điểm cực trị:
- Khi x < 0, y' > 0, hàm số đồng biến.
- Khi 0 < x < 2, y' < 0, hàm số nghịch biến.
- Khi x > 2, y' > 0, hàm số đồng biến.
Lưu ý khi giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
- Luôn kiểm tra điều kiện xác định của hàm số trước khi tính đạo hàm.
- Sử dụng các quy tắc tính đạo hàm một cách chính xác.
- Vẽ bảng biến thiên để trực quan hóa sự biến thiên của hàm số.
- Đọc kỹ đề bài và xác định đúng yêu cầu của bài toán.
Tài liệu tham khảo và hỗ trợ học tập
Ngoài sách giáo khoa và chuyên đề học tập, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
- Các trang web học Toán trực tuyến như tusach.vn, loigiaihay.com,...
- Các video bài giảng trên YouTube.
- Các bài tập trắc nghiệm và tự luận để rèn luyện kỹ năng.
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều và đạt kết quả tốt trong học tập.