Giải mục 2 trang 6, 7, 8, 9 Chuyên đề học tập Toán 11 - Cánh diều
Tổng quan nội dung
Giải mục 2 trang 6, 7, 8, 9 Chuyên đề học tập Toán 11 - Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 6, 7, 8, 9 của Chuyên đề học tập Toán 11, bộ sách Cánh Diều. Bài giải được các giáo viên có kinh nghiệm biên soạn, đảm bảo tính chính xác và logic.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho vectơ (vec u) và điểm M trong mặt phẳng.
Hoạt động 3
Cho phép tịnh tiến \({T_{\vec u}}\) và hai điểm M, N. Giả sử \(M' = {T_{\vec u}}\left( M \right),\,N' = {T_{\vec u}}\left( N \right)\)
a) Biểu diễn các vectơ \(\overrightarrow {MM'} \,\) và \(\overrightarrow {NN'} \) theo \(\vec u\).
b) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow {M'N'} \) và \(\overrightarrow {MN} \).
c) So sánh các đoạn thẳng M'N' và MN.
Phương pháp giải:
+ Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
+ Dựa vào quy tắc 3 điểm để làm
Lời giải chi tiết:
a) Vì \(M' = {T_{\vec u}}\left( M \right)\) nên \(\overrightarrow {MM'} = \vec u\).
Vì \(N' = {T_{\vec u}}\left( N \right)\) nên \(\overrightarrow {NN'} = \vec u\).
b) Theo quy tắc ba điểm ta có:
\(\overrightarrow {MN} = \overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {MM'} + \overrightarrow {M'N'} + \overrightarrow {N'N} = \vec u + \overrightarrow {M'N'} + \left( { - \overrightarrow {NN'} } \right) = \vec u + \overrightarrow {M'N'} + \left( { - \vec u} \right) = \overrightarrow {M'N'} \)Vậy \(\overrightarrow {MN} = \overrightarrow {M'N'} \).
c) Vì \(\overrightarrow {MN} = \overrightarrow {M'N'} \) nên MN = M'N'.
Luyện tập 2
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0) và bán kính R = 3. Xác định ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\)
Phương pháp giải:
Xác định ảnh của tâm O qua phép tịnh tiến bằng cách:
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Sau đó xác định ảnh của đường tròn qua phép tịnh tiến.
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\) là một đường tròn bán kính bằng 3, gọi là (C').
Gọi O' là tâm của (C'). Ta có O' là ảnh của O qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\) nên \(\overrightarrow {OO'} = \vec u = \left( {3;\,4} \right)\). Suy ra O'(3; 4).
Vậy ảnh của đường tròn (C) là đường tròn (C') có tâm O'(3; 4), bán kính bằng 3.
Hoạt động 2
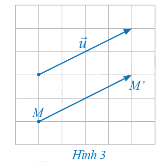
Cho vectơ \(\vec u\) và điểm M trong mặt phẳng. Hãy xác định điểm M' trong mặt phẳng sao cho \(\overrightarrow {MM'} = \vec u\) (Hình 3).
Phương pháp giải:
Quan sát hình 3, xác định điểm M' thỏa mãn \(\overrightarrow {MM'} = \vec u\)
Lời giải chi tiết:
Cách xác định điểm M' trong mặt phẳng sao cho: \(\overrightarrow {MM'} = \vec u\)
- Qua M kẻ đường thẳng d song song với giá của vectơ (hoặc trùng với giá của vectơ \(\vec u\) nếu điểm M thuộc giá của vectơ \(\vec u\)).
- Trên đường thẳng d, lấy điểm M' sao cho \(MM' = \left( {\vec u} \right)\), và hướng từ M đến M' cùng hướng với vectơ \(\vec u\). (Tham khảo Hình 3)
Luyện tập 1
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} .\)
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
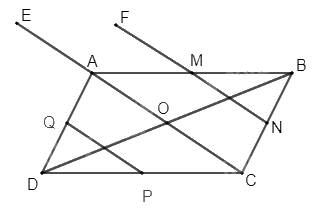
+ Vì M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và MN = AC. Do đó, \(\overrightarrow {NM} = \frac{1}{2}\overrightarrow {CA} \,\,(1)\).Vì O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC, do đó \(OA = \frac{1}{2}AC\). Suy ra \(\overrightarrow {OA} = \frac{1}{2}\overrightarrow {CA} \) (2).
Từ (1) và (2) suy ra \(\overrightarrow {NM} = \overrightarrow {OA} \,\,(3)\)
Vậy ảnh của điểm N qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm M.
+ Vì P và Q lần lượt là trung điểm của CD và DA nên PQ là đường trung bình của tam giác ADC, suy ra PQ // AC và \(PQ = \frac{1}{2}AC\). Do đó, \(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CA} \) (4)
Từ (2) và (4) suy ra \(\overrightarrow {PQ} = \overrightarrow {OA} \)
Vậy ảnh của điểm P qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm Q.
+ Vì O là trung điểm của AC nên \(\overrightarrow {CO} = \overrightarrow {OA} \).
Vậy ảnh của điểm C qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm O.
+ Lấy điểm E đối xứng với điểm O qua điểm A, khi đó A là trung điểm của OE.
Suy ra \(\overrightarrow {AE} = \overrightarrow {OA} \).
Vậy ảnh của điểm A qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm E.
+ Lấy điểm F đối xứng với điểm N qua điểm M, khi đó M là trung điểm của NF.
Suy ra \(\overrightarrow {NM} = \overrightarrow {MF} \,\,(5)\)
Từ (3) và (5) suy ra \(\overrightarrow {MF} = \overrightarrow {OA} \).
Vậy ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \)
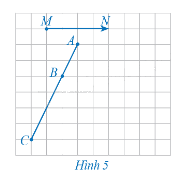
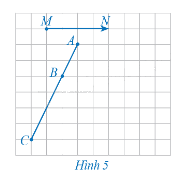
Hoạt động 4
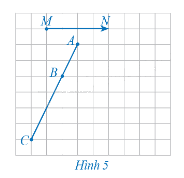
Xét phép tịnh tiến theo vectơ \(\overrightarrow {MN} \) (Hình 5).
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép tịnh tiến trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
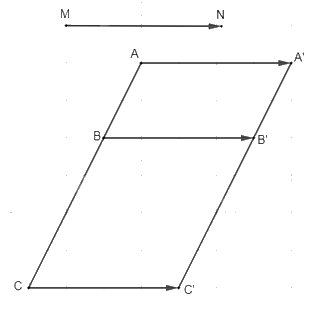
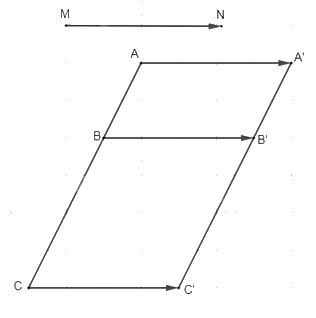
a) Vì A', B', C' lần lượt là ảnh của các điểm A, B, C qua phép tịnh tiến theo vectơ \(\overrightarrow {MN} \) nên ta xác định các điểm A', B', C' bằng cách lấy các điểm đó thỏa mãn: \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {BB'} = \overrightarrow {MN} ,\,\overrightarrow {CC'} = \overrightarrow {MN} \) (như hình vẽ trên).
b) Vì \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {BB'} = \overrightarrow {MN} \) nên \(\overrightarrow {AA'} = \overrightarrow {BB'} \), suy ra ABB'A' là hình bình hành.
Do đó, \(\overrightarrow {AB} = \overrightarrow {A'B'} \,\,(1)\)
Vì \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {CC'} = \overrightarrow {MN} \) nên \(\overrightarrow {AA'} = \overrightarrow {CC'} \), suy ra ACC'A' là hình bình hành.
Do đó, \(\overrightarrow {AC} = \overrightarrow {A'C'} \,\,(2)\)
Vì A, B, C là 3 điểm thẳng hàng với B nằm giữa A và C nên \(\overrightarrow {AB} = k\overrightarrow {AC} \,\,(k \ne 0)\) (3).
Từ (1), (2) và (3) suy ra \(\overrightarrow {A'B'} = k\overrightarrow {A'C'} \)
Vậy ba điểm A', B', C' thẳng hàng với B' nằm giữa A' và C'.
- Hoạt động 2
- Luyện tập 1
- Hoạt động 3
- Hoạt động 4
- Luyện tập 2
Cho vectơ \(\vec u\) và điểm M trong mặt phẳng. Hãy xác định điểm M' trong mặt phẳng sao cho \(\overrightarrow {MM'} = \vec u\) (Hình 3).
Phương pháp giải:
Quan sát hình 3, xác định điểm M' thỏa mãn \(\overrightarrow {MM'} = \vec u\)
Lời giải chi tiết:
Cách xác định điểm M' trong mặt phẳng sao cho: \(\overrightarrow {MM'} = \vec u\)
- Qua M kẻ đường thẳng d song song với giá của vectơ (hoặc trùng với giá của vectơ \(\vec u\) nếu điểm M thuộc giá của vectơ \(\vec u\)).
- Trên đường thẳng d, lấy điểm M' sao cho \(MM' = \left( {\vec u} \right)\), và hướng từ M đến M' cùng hướng với vectơ \(\vec u\). (Tham khảo Hình 3)
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} .\)
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
+ Vì M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và MN = AC. Do đó, \(\overrightarrow {NM} = \frac{1}{2}\overrightarrow {CA} \,\,(1)\).Vì O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC, do đó \(OA = \frac{1}{2}AC\). Suy ra \(\overrightarrow {OA} = \frac{1}{2}\overrightarrow {CA} \) (2).
Từ (1) và (2) suy ra \(\overrightarrow {NM} = \overrightarrow {OA} \,\,(3)\)
Vậy ảnh của điểm N qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm M.
+ Vì P và Q lần lượt là trung điểm của CD và DA nên PQ là đường trung bình của tam giác ADC, suy ra PQ // AC và \(PQ = \frac{1}{2}AC\). Do đó, \(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CA} \) (4)
Từ (2) và (4) suy ra \(\overrightarrow {PQ} = \overrightarrow {OA} \)
Vậy ảnh của điểm P qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm Q.
+ Vì O là trung điểm của AC nên \(\overrightarrow {CO} = \overrightarrow {OA} \).
Vậy ảnh của điểm C qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm O.
+ Lấy điểm E đối xứng với điểm O qua điểm A, khi đó A là trung điểm của OE.
Suy ra \(\overrightarrow {AE} = \overrightarrow {OA} \).
Vậy ảnh của điểm A qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm E.
+ Lấy điểm F đối xứng với điểm N qua điểm M, khi đó M là trung điểm của NF.
Suy ra \(\overrightarrow {NM} = \overrightarrow {MF} \,\,(5)\)
Từ (3) và (5) suy ra \(\overrightarrow {MF} = \overrightarrow {OA} \).
Vậy ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \)
Cho phép tịnh tiến \({T_{\vec u}}\) và hai điểm M, N. Giả sử \(M' = {T_{\vec u}}\left( M \right),\,N' = {T_{\vec u}}\left( N \right)\)
a) Biểu diễn các vectơ \(\overrightarrow {MM'} \,\) và \(\overrightarrow {NN'} \) theo \(\vec u\).
b) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow {M'N'} \) và \(\overrightarrow {MN} \).
c) So sánh các đoạn thẳng M'N' và MN.
Phương pháp giải:
+ Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
+ Dựa vào quy tắc 3 điểm để làm
Lời giải chi tiết:
a) Vì \(M' = {T_{\vec u}}\left( M \right)\) nên \(\overrightarrow {MM'} = \vec u\).
Vì \(N' = {T_{\vec u}}\left( N \right)\) nên \(\overrightarrow {NN'} = \vec u\).
b) Theo quy tắc ba điểm ta có:
\(\overrightarrow {MN} = \overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {MM'} + \overrightarrow {M'N'} + \overrightarrow {N'N} = \vec u + \overrightarrow {M'N'} + \left( { - \overrightarrow {NN'} } \right) = \vec u + \overrightarrow {M'N'} + \left( { - \vec u} \right) = \overrightarrow {M'N'} \)Vậy \(\overrightarrow {MN} = \overrightarrow {M'N'} \).
c) Vì \(\overrightarrow {MN} = \overrightarrow {M'N'} \) nên MN = M'N'.
Xét phép tịnh tiến theo vectơ \(\overrightarrow {MN} \) (Hình 5).
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép tịnh tiến trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
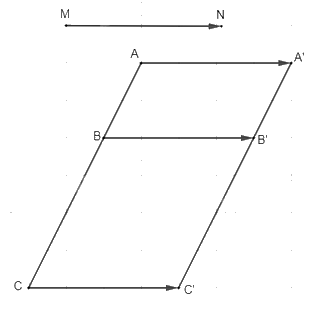
a) Vì A', B', C' lần lượt là ảnh của các điểm A, B, C qua phép tịnh tiến theo vectơ \(\overrightarrow {MN} \) nên ta xác định các điểm A', B', C' bằng cách lấy các điểm đó thỏa mãn: \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {BB'} = \overrightarrow {MN} ,\,\overrightarrow {CC'} = \overrightarrow {MN} \) (như hình vẽ trên).
b) Vì \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {BB'} = \overrightarrow {MN} \) nên \(\overrightarrow {AA'} = \overrightarrow {BB'} \), suy ra ABB'A' là hình bình hành.
Do đó, \(\overrightarrow {AB} = \overrightarrow {A'B'} \,\,(1)\)
Vì \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {CC'} = \overrightarrow {MN} \) nên \(\overrightarrow {AA'} = \overrightarrow {CC'} \), suy ra ACC'A' là hình bình hành.
Do đó, \(\overrightarrow {AC} = \overrightarrow {A'C'} \,\,(2)\)
Vì A, B, C là 3 điểm thẳng hàng với B nằm giữa A và C nên \(\overrightarrow {AB} = k\overrightarrow {AC} \,\,(k \ne 0)\) (3).
Từ (1), (2) và (3) suy ra \(\overrightarrow {A'B'} = k\overrightarrow {A'C'} \)
Vậy ba điểm A', B', C' thẳng hàng với B' nằm giữa A' và C'.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0) và bán kính R = 3. Xác định ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\)
Phương pháp giải:
Xác định ảnh của tâm O qua phép tịnh tiến bằng cách:
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Sau đó xác định ảnh của đường tròn qua phép tịnh tiến.
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\) là một đường tròn bán kính bằng 3, gọi là (C').
Gọi O' là tâm của (C'). Ta có O' là ảnh của O qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\) nên \(\overrightarrow {OO'} = \vec u = \left( {3;\,4} \right)\). Suy ra O'(3; 4).
Vậy ảnh của đường tròn (C) là đường tròn (C') có tâm O'(3; 4), bán kính bằng 3.
Giải mục 2 trang 6, 7, 8, 9 Chuyên đề học tập Toán 11 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 11 Cánh Diều thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng vào giải bài tập. Việc giải đúng và hiểu rõ các bài tập trong mục này là nền tảng quan trọng để tiếp thu kiến thức ở các phần sau. Tusach.vn sẽ cung cấp lời giải chi tiết cho từng bài tập trang 6, 7, 8, 9, kèm theo các lưu ý quan trọng và phương pháp giải hiệu quả.
Nội dung chính của Mục 2 (Trang 6, 7, 8, 9)
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định nội dung chính mà sách Cánh Diều trình bày. Thông thường, mục này sẽ bao gồm:
- Lý thuyết trọng tâm: Các định nghĩa, tính chất, định lý liên quan đến chủ đề.
- Ví dụ minh họa: Các bài toán mẫu giúp học sinh hiểu cách áp dụng lý thuyết vào thực tế.
- Bài tập luyện tập: Các bài tập từ dễ đến khó, giúp học sinh rèn luyện kỹ năng giải toán.
Giải chi tiết bài tập trang 6
Bài 1: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Bài 2: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Giải chi tiết bài tập trang 7
Bài 3: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Bài 4: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Giải chi tiết bài tập trang 8
Bài 5: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Bài 6: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Giải chi tiết bài tập trang 9
Bài 7: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Bài 8: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: ...
Mẹo giải Toán 11 Cánh Diều hiệu quả
- Nắm vững lý thuyết: Đọc kỹ sách giáo khoa, ghi chép các công thức và định lý quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng tài liệu tham khảo: Tham khảo các sách bài tập, đề thi thử để mở rộng kiến thức.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo để được hướng dẫn.
Kết luận
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Mục 2 trang 6, 7, 8, 9 Chuyên đề học tập Toán 11 Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 6 | Dễ |
| Bài 2 | 6 | Trung bình |
| Bài 3 | 7 | Trung bình |