Giải mục 2 trang 14, 15, 16 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải mục 2 trang 14, 15, 16 Chuyên đề học tập Toán 12 - Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 14, 15, 16 trong Chuyên đề học tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12 Cánh Diều, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
a) Xét phép thử (T): “Tung một đồng xu cân đối và đồng chất một lần”. Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Viết không gian mẫu (Omega ) của phép thử (T). b) Xét phép thử ({T_1}): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” (({T_1}) còn được gọi là phép thử lặp và việc tung một đồng xu hai lần liên tiếp một cách độc lập được hiểu là kết quả có thể xảy ra của lần thứ hai không phụ thuộc vào kết quả có thể xảy ra của tung lần
Hoạt động 2
Trả lời câu hỏi Hoạt động 2 trang 14 Chuyên đề học tập Toán 12 Cánh diều
a) Xét phép thử \(T\): “Tung một đồng xu cân đối và đồng chất một lần”. Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Viết không gian mẫu \(\Omega \) của phép thử \(T\).
b) Xét phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” (\({T_1}\) còn được gọi là phép thử lặp và việc tung một đồng xu hai lần liên tiếp một cách độc lập được hiểu là kết quả có thể xảy ra của lần thứ hai không phụ thuộc vào kết quả có thể xảy ra của tung lần thứ nhất).
Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu sau hai lần tung. Viết không gian mẫu \({\Omega _1}\) của phép thử \({T_1}\).
c) Trong phép thử lặp \({T_1}\) ta xét các biến cố:
\({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung”;
\({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung”;
\({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung”;
- Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)
- Với mỗi \(k = 0;1;2\) hãy so sánh: \(P({A_k})\) với \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}}\)
Phương pháp giải:
a,b: liệt kê các kết quả có thể xảy ra của phép thử.
c: Liệt kê các kết quả xảy ra của các biến cố \({A_0};{A_1};{A_2}\) từ đó tính xác suất xảy ra của các biến cố \({A_0};{A_1};{A_2}\).
Lời giải chi tiết:
a) Khi gieo đồng xu cân đối đồng chất thì sẽ có 2 trường hợp xảy ra là xuất hiện mặt sấp và xuất hiện mặt ngửa nên ta có không gian mẫu của phép thử \(T\) là: \(\Omega = \left\{ {S;\left. N \right\}} \right.\)
b) Khi gieo đồng xu 2 lần liên tiếp thì có thể xuất hiện 2 mặt sấp hoặc 2 mặt ngửa hoặc một mặt sấp một mặt ngửa nên ta có không gian mẫu của phép thử \({T_1}\) là: \({\Omega _1} = \{ SS;SN;NS;NN\} \)
c) Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)
Ta có biến cố \({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung” nên ta có
\({A_0} = \{ NN\} \) \( \Rightarrow n({A_0}) = 1 \Rightarrow P({A_0}) = \frac{{n({A_0})}}{{n({\Omega _1})}} = \frac{1}{4}\)
Ta có biến cố \({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung” nên ta có
\(\) \({A_1} = \{ SN;NS\} \) \( \Rightarrow n({A_1}) = 2 \Rightarrow P({A_1}) = \frac{{n({A_1})}}{{n({\Omega _1})}} = \frac{2}{4} = \frac{1}{2}\)
Ta có biến cố \({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung” nên ta có
\({A_2} = \{ SS\} \) \( \Rightarrow n({A_2}) = 1 \Rightarrow P({A_2}) = \frac{{n({A_2})}}{{n({\Omega _1})}} = \frac{1}{4}\)
- Với mỗi \(k = 0;1;2\) hãy so sánh: \(P({A_k})\) với \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}}\)
+) Với \(k = 0\) ta có \(C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4} = P({A_0})\)
+) Với \(k = 1\) ta có \(C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2} = P({A_1})\)
+) Với \(k = 2\) ta có \(C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4} = P({A_2})\)
Vậy \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}} = P({A_k})\)
- Hoạt động 2
- Hoạt động 3
Trả lời câu hỏi Hoạt động 2 trang 14 Chuyên đề học tập Toán 12 Cánh diều
a) Xét phép thử \(T\): “Tung một đồng xu cân đối và đồng chất một lần”. Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Viết không gian mẫu \(\Omega \) của phép thử \(T\).
b) Xét phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” (\({T_1}\) còn được gọi là phép thử lặp và việc tung một đồng xu hai lần liên tiếp một cách độc lập được hiểu là kết quả có thể xảy ra của lần thứ hai không phụ thuộc vào kết quả có thể xảy ra của tung lần thứ nhất).
Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu sau hai lần tung. Viết không gian mẫu \({\Omega _1}\) của phép thử \({T_1}\).
c) Trong phép thử lặp \({T_1}\) ta xét các biến cố:
\({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung”;
\({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung”;
\({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung”;
- Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)
- Với mỗi \(k = 0;1;2\) hãy so sánh: \(P({A_k})\) với \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}}\)
Phương pháp giải:
a,b: liệt kê các kết quả có thể xảy ra của phép thử.
c: Liệt kê các kết quả xảy ra của các biến cố \({A_0};{A_1};{A_2}\) từ đó tính xác suất xảy ra của các biến cố \({A_0};{A_1};{A_2}\).
Lời giải chi tiết:
a) Khi gieo đồng xu cân đối đồng chất thì sẽ có 2 trường hợp xảy ra là xuất hiện mặt sấp và xuất hiện mặt ngửa nên ta có không gian mẫu của phép thử \(T\) là: \(\Omega = \left\{ {S;\left. N \right\}} \right.\)
b) Khi gieo đồng xu 2 lần liên tiếp thì có thể xuất hiện 2 mặt sấp hoặc 2 mặt ngửa hoặc một mặt sấp một mặt ngửa nên ta có không gian mẫu của phép thử \({T_1}\) là: \({\Omega _1} = \{ SS;SN;NS;NN\} \)
c) Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)
Ta có biến cố \({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung” nên ta có
\({A_0} = \{ NN\} \) \( \Rightarrow n({A_0}) = 1 \Rightarrow P({A_0}) = \frac{{n({A_0})}}{{n({\Omega _1})}} = \frac{1}{4}\)
Ta có biến cố \({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung” nên ta có
\(\) \({A_1} = \{ SN;NS\} \) \( \Rightarrow n({A_1}) = 2 \Rightarrow P({A_1}) = \frac{{n({A_1})}}{{n({\Omega _1})}} = \frac{2}{4} = \frac{1}{2}\)
Ta có biến cố \({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung” nên ta có
\({A_2} = \{ SS\} \) \( \Rightarrow n({A_2}) = 1 \Rightarrow P({A_2}) = \frac{{n({A_2})}}{{n({\Omega _1})}} = \frac{1}{4}\)
- Với mỗi \(k = 0;1;2\) hãy so sánh: \(P({A_k})\) với \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}}\)
+) Với \(k = 0\) ta có \(C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4} = P({A_0})\)
+) Với \(k = 1\) ta có \(C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2} = P({A_1})\)
+) Với \(k = 2\) ta có \(C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4} = P({A_2})\)
Vậy \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}} = P({A_k})\)
Trả lời câu hỏi Hoạt động 3 trang 16 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử lặp \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập”. Gọi \(X\) là số lần mặt ngửa xuất hiện sau hai lần tung.
Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\).
Phương pháp giải:
+) \(X\) là số lần xuất hiện mặt ngửa của phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” nên \(X\) sẽ nhận các giá trị 0;1;2
+) Ta sẽ tính các xác suất: \(P(X = 0);P(X = 1);P(X = 2)\)
Lời giải chi tiết:
Gieo một đồng xu cân đối đồng chất hai lần liên tiếp thì có các khả năng sau xảy ra : \(SS;SN;NS;NN\)
Gọi \({A_k}\) là biến cố “Mặt ngửa xuất hiện đúng \(k\) lần” \(k = 0;1;2\).
Vì xác suất xuất hiện mặt ngửa trong một lần tung là \(\frac{1}{2}\) nên ta áp dụng công thức Bernoulli với \(p = \frac{1}{2}\) và \(k = 0;1;2\) ta có:
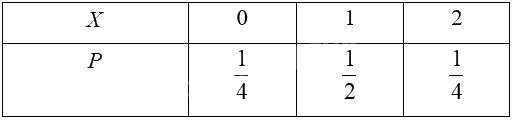
\(P(X = 0) = P({A_0}) = C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4}\);
\(P(X = 1) = P({A_1}) = C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2}\)
\(P(X = 2) = P({A_2}) = C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4}\)
Ta có bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) như sau:
Hoạt động 3
Trả lời câu hỏi Hoạt động 3 trang 16 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử lặp \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập”. Gọi \(X\) là số lần mặt ngửa xuất hiện sau hai lần tung.
Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\).
Phương pháp giải:
+) \(X\) là số lần xuất hiện mặt ngửa của phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” nên \(X\) sẽ nhận các giá trị 0;1;2
+) Ta sẽ tính các xác suất: \(P(X = 0);P(X = 1);P(X = 2)\)
Lời giải chi tiết:
Gieo một đồng xu cân đối đồng chất hai lần liên tiếp thì có các khả năng sau xảy ra : \(SS;SN;NS;NN\)
Gọi \({A_k}\) là biến cố “Mặt ngửa xuất hiện đúng \(k\) lần” \(k = 0;1;2\).
Vì xác suất xuất hiện mặt ngửa trong một lần tung là \(\frac{1}{2}\) nên ta áp dụng công thức Bernoulli với \(p = \frac{1}{2}\) và \(k = 0;1;2\) ta có:
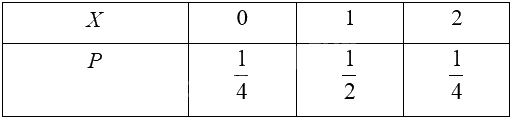
\(P(X = 0) = P({A_0}) = C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4}\);
\(P(X = 1) = P({A_1}) = C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2}\)
\(P(X = 2) = P({A_2}) = C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4}\)
Ta có bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) như sau:
Giải mục 2 trang 14, 15, 16 Chuyên đề học tập Toán 12 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 2 trang 14, 15, 16 trong Chuyên đề học tập Toán 12 Cánh Diều tập trung vào một phần quan trọng của chương trình, thường liên quan đến một chủ đề cụ thể trong giải tích hoặc hình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức nền tảng, hiểu rõ các định nghĩa, định lý và công thức liên quan.
Nội dung chính của Mục 2
Thông thường, Mục 2 sẽ bao gồm các nội dung sau:
- Lý thuyết trọng tâm: Tóm tắt các khái niệm, định lý, quy tắc cần thiết để giải bài tập.
- Ví dụ minh họa: Các bài toán mẫu được giải chi tiết, giúp học sinh hiểu rõ phương pháp giải.
- Bài tập luyện tập: Các bài tập với mức độ khó tăng dần, giúp học sinh rèn luyện kỹ năng và củng cố kiến thức.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 14, 15, 16:
Bài 1: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng)
Bài 2: (Bài tập luyện tập)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng)
Các lưu ý khi giải bài tập
Để đạt hiệu quả cao trong quá trình giải bài tập, học sinh cần lưu ý những điều sau:
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài toán trước khi bắt đầu giải.
- Xác định kiến thức cần sử dụng: Lựa chọn các định lý, công thức phù hợp để giải bài toán.
- Trình bày lời giải rõ ràng, logic: Viết các bước giải một cách mạch lạc, dễ hiểu.
- Kiểm tra lại kết quả: Đảm bảo kết quả cuối cùng là chính xác.
Tusach.vn – Hỗ trợ học tập Toán 12 hiệu quả
Tusach.vn là một nguồn tài liệu học tập Toán 12 uy tín và chất lượng. Chúng tôi cung cấp:
- Lời giải chi tiết các bài tập: Giải thích rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức.
- Bài giảng video: Trình bày trực quan, sinh động, giúp học sinh dễ dàng tiếp thu kiến thức.
- Bài tập trắc nghiệm: Giúp học sinh rèn luyện kỹ năng làm bài trắc nghiệm.
- Diễn đàn trao đổi: Nơi học sinh có thể trao đổi, thảo luận và giải đáp thắc mắc.
Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kết quả học tập của bạn!
Bảng tóm tắt các công thức quan trọng (Ví dụ)
| Công thức | Mô tả |
|---|---|
| (Ví dụ công thức 1) | (Mô tả công thức 1) |
| (Ví dụ công thức 2) | (Mô tả công thức 2) |
Chúc các bạn học tập tốt và đạt kết quả cao trong môn Toán 12!