Giải bài 2 trang 35 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 2 trang 35 Chuyên đề học tập Toán 12 - Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 2 trang 35 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất.
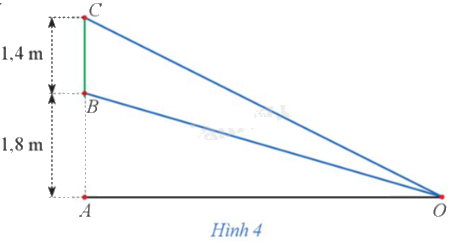
Hình 4 minh hoạ một màn hình (BC) có chiều cao 1,4 m được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng (BA = 1,8)m. Một chiếc đèn quan sát màn hình được đặt ở vị trí (O) trên mặt đất. Hãy tính khoảng cách (AO) sao cho góc quan sát (BOC) là lớn nhất.
Đề bài
Hình 4 minh hoạ một màn hình \(BC\) có chiều cao 1,4 m được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng \(BA = 1,8\)m. Một chiếc đèn quan sát màn hình được đặt ở vị trí \(O\) trên mặt đất. Hãy tính khoảng cách \(AO\) sao cho góc quan sát \(BOC\) là lớn nhất.
Phương pháp giải - Xem chi tiết
+) Do góc \(\widehat {BOC}\)là góc của tam giác nên \({0^0} < \widehat {BOC} < {180^0}\)khi đó \(\widehat {BOC}\)càng lớn thì \(\tan \widehat {BOC}\)cũng càng lớn nên ta sẽ đưa về tìm AO để \(\tan \widehat {BOC}\)lớn nhất.
+) Ta cần biểu thị \(\tan \widehat {BOC}\)qua các đoạn thẳng đã và qua AO. Sử dụng công thức:
\(\tan (a - b) = \frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}\); trong đó \(\widehat {BOC} = \widehat {AOC} - \widehat {AOB}\)
+) Ta được \(\tan \widehat {BOC}\)được tính bằng 1 biểu thức chứa \(x\). Khi đó ta xét hàm số tương ứng và tìm giá trị lớn nhất của nó.
Lời giải chi tiết
Để góc quan sát \(\widehat {BOC}\) lớn nhất thì \(\tan \widehat {BOC}\) là lớn nhất.
Giả sử \(AO = x\) (m) \((x > 0).\)
Ta có \(\tan \widehat {BOC} = \tan (\widehat {AOC} - \widehat {AOB}) = \frac{{\tan \widehat {AOC} - \tan \widehat {AOB}}}{{1 + \tan \widehat {AOC}.\tan \widehat {AOB}}}\)
\(\tan \widehat {BOC} = \frac{{\frac{{AC}}{{AO}} - \frac{{AB}}{{AO}}}}{{1 + \frac{{AC}}{{AO}}.\frac{{AB}}{{AO}}}} = \frac{{\frac{{1,4}}{x}}}{{1 + \frac{{1,8 + 1,4}}{x}.\frac{{1,8}}{x}}} = \frac{{1,4x}}{{{x^2} + 5,76}}.\)
Xét hàm số \(f(x) = \frac{{1,4x}}{{{x^2} + 5,76}},\) \(x \in (0; + \infty ).\)
Ta có \(f'(x) = \frac{{1,4({x^2} + 5,76) - 1,4x.2x}}{{{{\left( {{x^2} + 5,76} \right)}^2}}} = \frac{{ - 1,4{x^2} + 8,064}}{{{{\left( {{x^2} + 5,76} \right)}^2}}}.\)
Do đó \(f'(x) = 0 \Leftrightarrow x = 2,4\) (do \(x > 0\)).
Bảng biến thiên của hàm số:
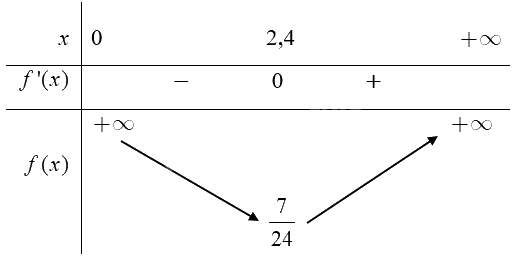
Căn cứ vào bảng biến thiên ta có \(\mathop {\max }\limits_{(0; + \infty )} f(x) = f(2,4) = \frac{7}{{24}}\) tại \(x = 2,4.\)
Vậy để góc quan sát \(\widehat {BOC}\) lớn nhất thì khoảng cách \(AO = 2,4\) mét.
Giải bài 2 trang 35 Chuyên đề học tập Toán 12 - Cánh diều: Tổng quan và Phương pháp giải
Bài 2 trang 35 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, tìm cực trị, và khảo sát sự biến thiên của hàm số. Việc nắm vững các khái niệm và công thức đạo hàm là yếu tố then chốt để giải quyết bài toán này một cách hiệu quả.
Nội dung chi tiết bài 2 trang 35
Bài 2 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tìm đạo hàm của hàm số: Học sinh cần thành thạo các quy tắc đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương, và đạo hàm của hàm hợp.
- Dạng 2: Tìm cực trị của hàm số: Học sinh cần tìm các điểm mà đạo hàm bằng 0 hoặc không tồn tại, sau đó xét dấu đạo hàm để xác định cực đại, cực tiểu.
- Dạng 3: Khảo sát sự biến thiên của hàm số: Học sinh cần xác định khoảng đồng biến, nghịch biến, cực trị, và giới hạn của hàm số để vẽ đồ thị hàm số.
Lời giải chi tiết bài 2 trang 35 (Ví dụ minh họa)
Đề bài: Cho hàm số y = x3 - 3x2 + 2. Tìm cực đại và cực tiểu của hàm số.
Lời giải:
- Bước 1: Tính đạo hàm: y' = 3x2 - 6x
- Bước 2: Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
- Bước 3: Xét dấu đạo hàm:
- Với x < 0, y' > 0, hàm số đồng biến.
- Với 0 < x < 2, y' < 0, hàm số nghịch biến.
- Với x > 2, y' > 0, hàm số đồng biến.
- Bước 4: Kết luận: Hàm số đạt cực đại tại x = 0, ymax = 2 và đạt cực tiểu tại x = 2, ymin = -2.
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
- Nắm vững các quy tắc đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra kết quả.
- Tham khảo các tài liệu tham khảo và lời giải chi tiết trên các trang web uy tín như tusach.vn.
Tầm quan trọng của việc giải bài tập Chuyên đề học tập Toán 12
Việc giải bài tập Chuyên đề học tập Toán 12 không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề và tư duy logic. Đây là những kỹ năng cần thiết để thành công trong học tập và công việc sau này. Ngoài ra, việc làm quen với các dạng bài tập thường gặp trong các kỳ thi THPT Quốc gia sẽ giúp học sinh tự tin hơn khi làm bài thi.
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách giáo khoa và Chuyên đề học tập Toán 12. Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 12 | https://tusach.vn/giai-bai-tap-toan-12 |
| Chuyên đề học tập Toán 12 | https://tusach.vn/chuyen-de-hoc-tap-toan-12 |