Giải bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất.
Một cơ sở sản xuất đồ gỗ dự định sản xuất ba loại sả phẩm là bàn, ghế và tủ. Định mức sử dụng lao động, chi phí sản suất và giá bán mỗi sản phẩm mỗi loại ước tính trong Bảng 4: Biết rằng cơ sở sản xuất đó sử dụng không quá 500 ngày công, số tiền dành cho chi phí sản xuất không quá 40 triệu đồng và số ghế gấp sáu lần số bàn. Tính số sản phẩm mỗi loại cần phải sản xuất sao cho tổng doanh thu đạt được cao nhất.
Đề bài
Một cơ sở sản xuất đồ gỗ dự định sản xuất ba loại sả phẩm là bàn, ghế và tủ. Định mức sử dụng lao động, chi phí sản suất và giá bán mỗi sản phẩm mỗi loại ước tính trong Bảng 4:

Biết rằng cơ sở sản xuất đó sử dụng không quá 500 ngày công, số tiền dành cho chi phí sản xuất không quá 40 triệu đồng và số ghế gấp sáu lần số bàn. Tính số sản phẩm mỗi loại cần phải sản xuất sao cho tổng doanh thu đạt được cao nhất.
Phương pháp giải - Xem chi tiết
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{a_1}x + {b_1}y \le {c_1}\\{a_2}x + {b_2}y \le {c_2}\\...\\{a_k}x + {b_k}y \le {c_k}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết
Đổi 40 triệu đồng= 40 000 nghìn đồng.
Gọi \(x,y\) lần lượt là số chiếc bàn và số chiếc tủ cần sản cuất \((x \in N;y \in N)\)
Số chiếc ghế cần sản xuất là \(6x\) (chiếc)
Tổng doanh thu đạt được là \(T = 260x + 120.6x + 600y = 980x + 600y\) (nghìn đồng).
Số công lao động cần dùng là \(2x + 1.6x + 3y = 8x + 3y\) (ngày công)
Vì công lao động không vượt quá 500 ngày công nên ta có: \(8x + 3y \le 500.\)
Chi phí sản xuất các sản phẩm là \(100x + 40.6x + 250y = 340x + 250y\) (nghìn đồng)
Vì chi phí sản xuất không vượt quá 40 triệu đồng=40 000 nghìn đồng nên ta có \(340x + 250y \le 40000\) hay \(34x + 25y \le 4000\)
Vì cần thu được tổng doanh thu lớn nhất nên ta có bài toán quy hoạch tuyến tính: \(\left\{ \begin{array}{l}\max (T = 980x + 600y)\\8x + 3y \le 500\\34x + 25y \le 4000\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực):
\(\left\{ \begin{array}{l}8x + 3y \le 500\\34x + 25y \le 4000\\x \ge 0\\y \ge 0\end{array} \right.\) (II)
 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 980x + 600y\) khi \((x,y)\) thoả mãn hệ bất phương trình (II)
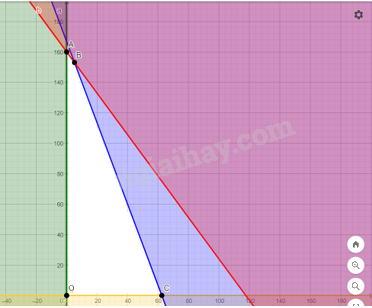
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh \(O(0;0);A(0;160);\) \(B\left( {\frac{{250}}{{49}};\frac{{7500}}{{49}}} \right);C(62,5;0)\).
Bước 2. Tính giá trị biểu thức \(T(x,y) = 980x + 600y\) tại các đỉnh của tứ giác OABC: \(T(0;0) = 0;T(0;160) = 96000;T\left( {\frac{{250}}{{49}};\frac{{7500}}{{49}}} \right) = \frac{{4745000}}{{49}};\) \(T(62,5;0) = 61250.\)
Bước 3. Ta đã biết biểu thức \(T = 980x + 600y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(0;160) = 96000.\)
Bước 4. Vì 0 và 160 là các số tự nhiên nên cặp số \((0;160)\) là nghiệm của bài toán (I).
Vậy chỉ cần sản xuất 160 chiếc tủ để tổng doanh thu đạt được là cao nhất.
Giải bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều: Tổng quan và Phương pháp giải
Bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về một chủ đề cụ thể. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm, định lý và công thức liên quan. Tusach.vn sẽ cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách tiếp cận và giải quyết vấn đề.
Nội dung bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Bài 4 thường bao gồm các dạng bài tập sau:
- Dạng 1: Bài tập về lý thuyết, yêu cầu học sinh trình bày các khái niệm, định lý.
- Dạng 2: Bài tập tính toán, yêu cầu học sinh áp dụng công thức để giải quyết.
- Dạng 3: Bài tập ứng dụng, yêu cầu học sinh vận dụng kiến thức vào thực tế.
Lời giải chi tiết bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
(Giả sử bài 4 là một bài toán về đạo hàm hàm số)
Đề bài: Cho hàm số y = f(x) = x3 - 3x2 + 2. Tính f'(x) và tìm các điểm cực trị của hàm số.
Lời giải:
- Tính đạo hàm f'(x):
- Tìm các điểm cực trị:
- Xác định loại cực trị:
- Khoảng (-∞, 0): f'(x) > 0, hàm số đồng biến.
- Khoảng (0, 2): f'(x) < 0, hàm số nghịch biến.
- Khoảng (2, +∞): f'(x) > 0, hàm số đồng biến.
- Tính giá trị cực đại, cực tiểu:
f'(x) = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của f'(x) trên các khoảng:
Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
f(0) = 2 (cực đại)
f(2) = -2 (cực tiểu)
Mẹo giải bài tập Toán 12 hiệu quả
Để học tốt môn Toán 12 và giải quyết các bài tập một cách hiệu quả, bạn nên:
- Nắm vững kiến thức lý thuyết.
- Luyện tập thường xuyên các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ học tập như máy tính bỏ túi, phần mềm giải toán.
- Tham khảo các tài liệu tham khảo, sách bài tập.
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn là website cung cấp lời giải bài tập Toán 12, Vật lý 12, Hóa học 12, Sinh học 12, Ngữ văn 12 và các môn học khác. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các giải pháp học tập hiệu quả nhất cho học sinh. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 12 | https://tusach.vn/toan-12 |
| Chuyên đề học tập Toán 12 | https://tusach.vn/chuyen-de-toan-12 |