Đề bài
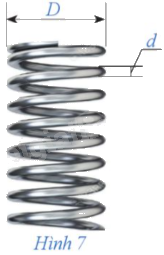
Một lò xo được làm từ một sợi dây kim loại. Gọi \(d\) là đường kính (trung bình) của sợ dây kim loại và \(D\) là đường kính (trung bình) của lò xo (Hình 7). Ki lò xo đứng lên mặt đất thì nó nén lại bởi trọng lượng \(P\) của lò xo, vật chất trong dây kim loại chịu ứng suất lớn nhất \(S\) tại các điểm trên bè mặt sợi dây mà khoảng cách từ những điểm đó đến đường tâm của lò so là nhỏ nhất.
Biết rằng \(S\) được cho bởi công thức:
\(S = \frac{{8PD}}{{\pi {d^3}}}\left[ {\frac{{\frac{{4D}}{d} - 1}}{{4\left( {\frac{D}{d} - 1} \right)}} + \frac{{0,615d}}{D}} \right].\)
a) Giả sử sợi dây kim loại là cố định. Hỏi ta phải cuộn sợi dây kim loại đó thành lò xo với đường kình \(D\) bằng bao nhiêu để ứng xuất \(S\) là nhỏ nhất?
b) Giả sử lò xo có đường kính \(D\) cố định. Hỏi ta phải chọn loại dây kim loại với đường kính \(d\) bằng bao nhiêu để ứng suất \(S\) là nhỏ nhất.
Phương pháp giải - Xem chi tiết
a) Khi sợi dây kim loại cố định thì \(d\) và \(P\) là các hằng số.
Khi đó, để dễ dàng trong tính toán ta đặt \(a = \frac{D}{d}(a > 0).\)
Biểu diễn lại \(S\) ta có: \(S(a) = \frac{{8Pa}}{{\pi {d^2}}}\left[ {\frac{{4a - 1}}{{4(a - 1)}} + \frac{{0,615}}{a}} \right] = \frac{{8P}}{{\pi {d^2}}}\left[ {\frac{{4{a^2} - a}}{{4(a - 1)}} + 0,615} \right]\)
Ta sẽ đi tìm giá trị nhỏ nhất của hàm số \(S(a)\).
b) Làm tương tự với câu a.
Lời giải chi tiết
a) Khi sợi dây kim loại cố định thì \(d\) và \(P\) là các hằng số.
Đặt \(a = \frac{D}{d}(a > 0).\)
Khi đó ta có hàm số \(S(a) = \frac{{8Pa}}{{\pi {d^2}}}\left[ {\frac{{4a - 1}}{{4(a - 1)}} + \frac{{0,615}}{a}} \right] = \frac{{8P}}{{\pi {d^2}}}\left[ {\frac{{4{a^2} - a}}{{4(a - 1)}} + 0,615} \right]\) với \(a > 0.\)
Ta có: \(S'(a) = \frac{{8P}}{{\pi {d^2}}}\left[ {\frac{{(8a - 1).4(a - 1) - (4{a^2} - a).4}}{{16{{(a - 1)}^2}}}} \right] = \frac{{2P}}{{\pi {d^2}}}.\frac{{4{a^2} - 8a + 1}}{{{{(a - 1)}^2}}}.\)
Do đó \(S'(a) = 0 \Leftrightarrow 4{a^2} - 8a + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}a = \frac{{2 - \sqrt 3 }}{2}\\a = \frac{{2 + \sqrt 3 }}{2}\end{array} \right.\)
Ta có bảng biến thiên:
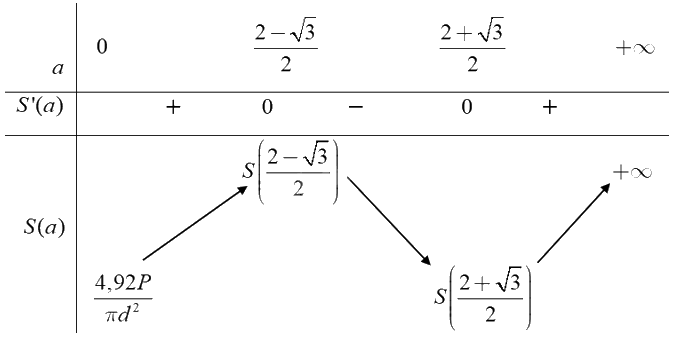
Căn cứ vào bảng biến thiên, ta có \(\mathop {\min }\limits_{(0; + \infty )} S(a) = S\left( {\frac{{2 + \sqrt 3 }}{2}} \right)\) tại \(a = \frac{{2 + \sqrt 3 }}{2}\) hay \(\frac{D}{d} = \frac{{2 + \sqrt 3 }}{2}\) suy ra \(D = \frac{{2 + \sqrt 3 }}{2}d.\)
b) Với \(d > 0\) ta có:
\(S(d) = \frac{{8PD}}{{\pi {D^2}}}\left[ {\frac{{4\frac{D}{d} - 1}}{{4\left( {\frac{D}{d} - 1} \right)}} + \frac{{0,615d}}{D}} \right] = \frac{{8P}}{{\pi {D^2}}}.{\left( {\frac{D}{d}} \right)^3}.\left[ {\frac{{4\frac{D}{d} - 1}}{{4\left( {\frac{D}{d} - 1} \right)}} + \frac{{0,615d}}{D}} \right]\)
Đặt \(a = \frac{D}{d}(a > 0).\)
Khi đó ta có hàm số \(S(a) = \frac{{8P{a^3}}}{{\pi {D^2}}}.\left[ {\frac{{4a - 1}}{{4\left( {a - 1} \right)}} + \frac{{0,615}}{a}} \right] = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{4{a^4} - {a^3}}}{{4\left( {a - 1} \right)}} + 0,615{a^2}} \right]\)
Ta có \(S'(a) = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{(16{a^3} - 3{a^2}).4(a - 1) - (4{a^4} - {a^3}).4}}{{16{{\left( {a - 1} \right)}^2}}} + 1,23a} \right]\)
\(S'(a) = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{12{a^4} - 18{a^3} + 3{a^2}}}{{4{{\left( {a - 1} \right)}^2}}} + 1,23a} \right] = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{12{a^4} - 18{a^3} + 3{a^2} + 1,23a.4{{\left( {a - 1} \right)}^2}}}{{4{{\left( {a - 1} \right)}^2}}}} \right]\)
\(S'(a) = \frac{{2P}}{{\pi {D^2}}}.\frac{{12{a^4} - 13,08{a^3} - 6,84{a^2} + 4,92a}}{{{{\left( {a - 1} \right)}^2}}}.\)
Do đó \(S'(a) = 0 \Leftrightarrow 12{a^4} - 13,08{a^3} - 6,84{a^2} + 4,92a = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0(ktm)\\x \approx 1,285\\x \approx 0,476\end{array} \right.\)
Ta có bảng biến thiên của hàm số:
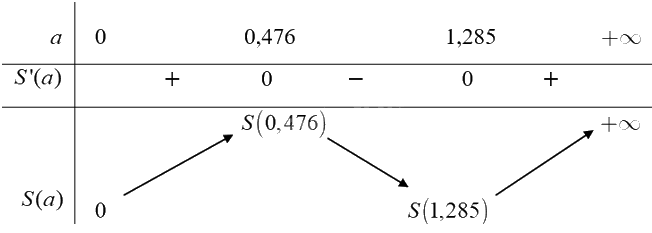
Căn cứ vào bảng biến thiên ta có \(\mathop {\min }\limits_{(0; + \infty )} S(a) = S(1,285)\) tại \(a \approx 1,285\) hay \(\frac{D}{d} \approx 1,285\) suy ra \(d \approx \frac{D}{{1,285}}.\)