Giải bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất.
Một doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6).
Đề bài
Một doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6).
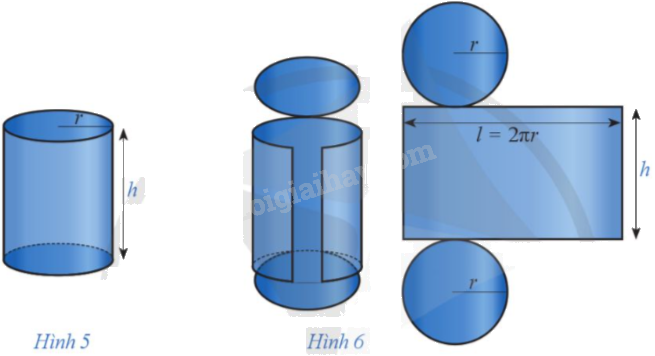
Phương pháp giải - Xem chi tiết
+) Từ thể tích của hộp đựng nước giải khát ta sẽ biểu diễn được chiều cao của hộp nước theo bán kính đáy của nó \(h = \frac{{500}}{{\pi {r^2}}}\)
+) Diện tích vỏ hộp chính là diện tích toàn phần của hộp nước hình trụ.
+) Ta sẽ biểu diễn được diện tích vỏ hộp bằng một hàm số \(S(r)\)ẩn r
+) Yêu cầu bài toán đồng nghĩa với việc ta phải đi tìm bán kính, chiều cao mà ở đó hàm số \(S(r)\)đạt giá trị nhỏ nhất.
Lời giải chi tiết
Chiều cao \(h\) của hộp đứng nước có dạng hình trụ là \(h = \frac{{500}}{{\pi {r^2}}}\) (cm).
Diện tích mặt đáy của hộp đựng nước là \({S_{\rm{d}}} = \pi {r^2}\) (\({\rm{c}}{{\rm{m}}^{\rm{2}}}\)).
Diện tích xung quanh của hộp đựng nước là \({S_{xq}} = 2\pi rh = 2\pi r.\frac{{500}}{{\pi {r^2}}} = \frac{{1000}}{r}{\rm{(c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Diện tích vỏ hộp là \(S = 2\pi {r^2} + \frac{{1000}}{r}({\rm{c}}{{\rm{m}}^{\rm{2}}})\).
Xét hàm số \(S(r) = 2\pi {r^2} + \frac{{1000}}{r},r \in (0; + \infty ).\)
Ta có \(S'(r) = 4\pi r - \frac{{1000}}{{{r^2}}}.\) Do đó \(S'(r) = 0 \Leftrightarrow r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}.\)
Ta có bảng biến thiên của hàm số \(S(r)\) như sau:
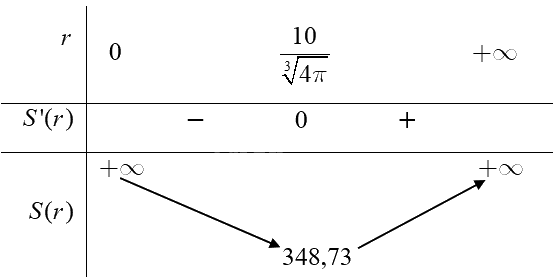
Căn cứ vào bảng biến thiên ta có \(\mathop {\min }\limits_{(0; + \infty )} S(r) \approx 348,73\) tại \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm).
Vậy để diện tích vỏ hộp là nhỏ nhất thì bán kính của chiếc hộp là \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm) và chiều cao của chiếc hộp là \(h = \frac{{500}}{{\pi {{\left( {\frac{{10}}{{\sqrt[3]{{4\pi }}}}} \right)}^2}}} = \frac{{5{{\left( {\sqrt[3]{{4\pi }}} \right)}^2}}}{\pi }\) (cm).
Giải bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều: Tổng quan và Phương pháp giải
Bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về một chủ đề cụ thể. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm, định lý và công thức liên quan. Tusach.vn sẽ cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách tiếp cận và giải quyết vấn đề.
Nội dung chi tiết bài 8 trang 37
Bài 8 thường bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các tình huống thực tế. Dưới đây là phân tích chi tiết về nội dung bài tập:
- Dạng 1: Bài tập về... (Ví dụ: Hàm số)
- Dạng 2: Bài tập về... (Ví dụ: Phương trình, Bất phương trình)
- Dạng 3: Bài tập về... (Ví dụ: Ứng dụng của đạo hàm)
Trong dạng bài tập này, học sinh cần xác định đúng loại hàm số, tìm tập xác định, tập giá trị, điểm cực trị và vẽ đồ thị hàm số. Tusach.vn sẽ hướng dẫn bạn cách sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra kết quả.
Để giải quyết dạng bài tập này, học sinh cần nắm vững các phương pháp giải phương trình, bất phương trình như phương pháp đặt ẩn phụ, phương pháp phân tích thành nhân tử, phương pháp sử dụng đồ thị. Chúng tôi sẽ cung cấp các ví dụ minh họa cụ thể để bạn dễ dàng hình dung.
Dạng bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, xét tính đơn điệu của hàm số. Tusach.vn sẽ giúp bạn hiểu rõ cách áp dụng đạo hàm vào các bài toán cụ thể.
Lời giải chi tiết bài 8 trang 37
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều:
- Câu a: ...
Lời giải: ...
- Câu b: ...
Lời giải: ...
- Câu c: ...
Lời giải: ...
Mẹo giải nhanh và hiệu quả
Để giải bài tập Toán 12 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của đề bài trước khi bắt đầu giải.
- Xác định đúng kiến thức cần sử dụng: Lựa chọn các khái niệm, định lý và công thức phù hợp để giải quyết bài tập.
- Sử dụng sơ đồ Venn hoặc bảng biểu: Giúp bạn tổ chức thông tin và tìm ra mối liên hệ giữa các yếu tố.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác và hợp lý.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa và chuyên đề học tập, bạn có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức:
- Sách bài tập Toán 12: Cung cấp nhiều bài tập đa dạng và phong phú.
- Các trang web học Toán trực tuyến: Tusach.vn, Vietjack, Hoc24,...
- Các video bài giảng Toán 12: Giúp bạn hiểu rõ hơn về các khái niệm và phương pháp giải.
Kết luận
Hy vọng rằng lời giải chi tiết bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều của Tusach.vn sẽ giúp bạn học tập tốt hơn và đạt kết quả cao trong kỳ thi. Chúc bạn thành công!